2.7 — External Economies & Industry Supply
ECON 306 • Microeconomic Analysis • Spring 2022
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/microS22
microS22.classes.ryansafner.com
Entry Effects & External Economies
Entry/Exit Effects on Market Price
When all firms produce more/less; or firms enter or exit an industry, this affects the equilibrium market price
Think about basic supply & demand graphs:
- Entry: \(\color{red}{\uparrow}\) industry supply \(\implies\) \(\uparrow q, \downarrow p\)
- Exit: \(\color{red}{\downarrow}\) industry supply \(\implies\) \(\downarrow q, \uparrow p\)
External Economies
How large this change in price will be from entry/exit depends on industry-wide costs and external economies
Economies of scale are internal to the firm (a firm's own average cost curve)
External economies have to do with how the size of the entire industry affects all individual firm's costs
- These are externalities that spill over across all firms in an industry
Constant Cost Industry (No External Economies) I
Constant cost industry has no external economies, no change in costs as industry output increases (firms enter & incumbents produce more)
A perfectly elastic long-run industry supply curve
Determinants:
- Industry's purchases are not a large share of input markets
- Often constant marginal costs, insignificant fixed costs
Examples: toothpicks, domain name registration, waitstaff


Constant Cost Industry (No External Economies) II
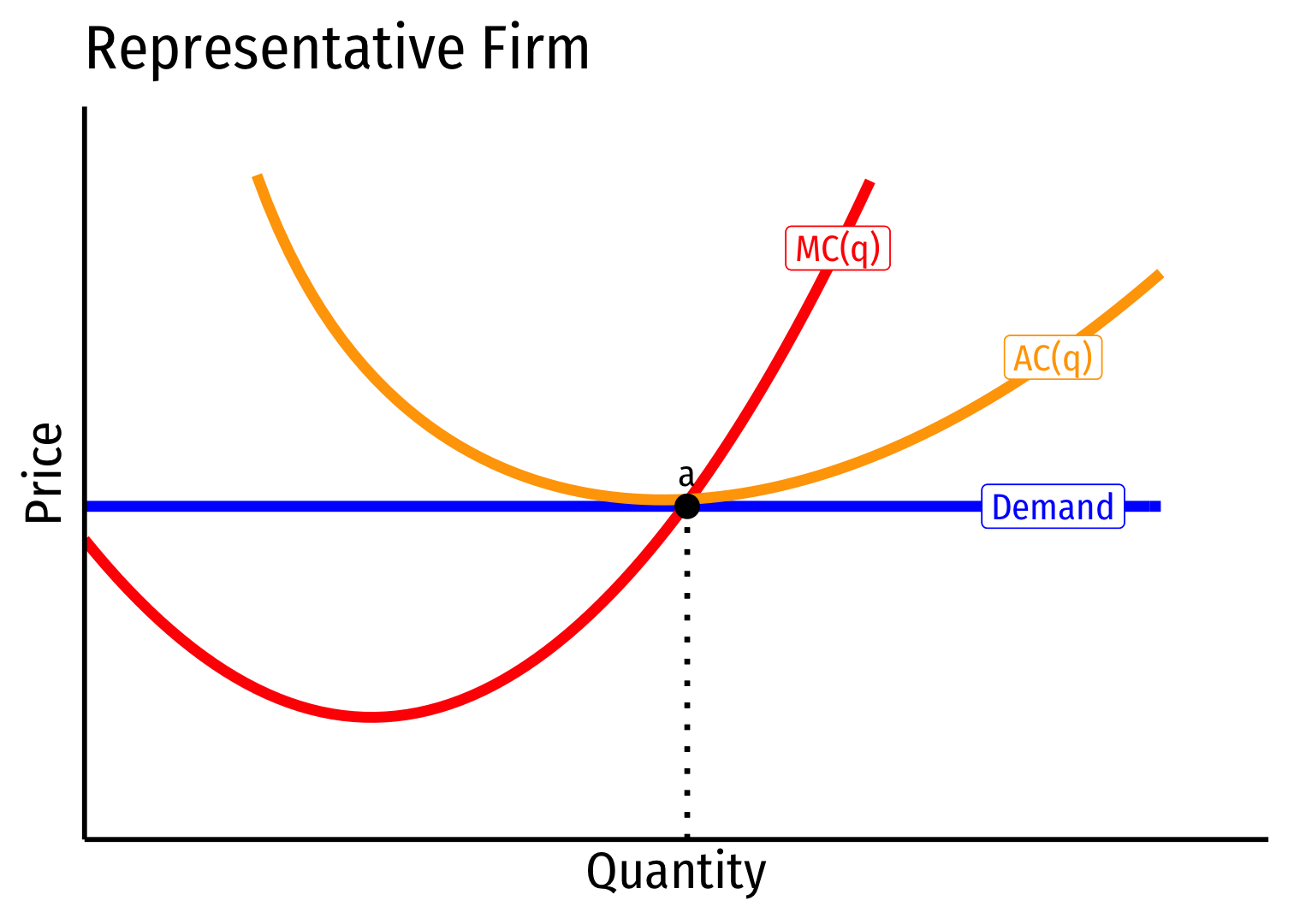
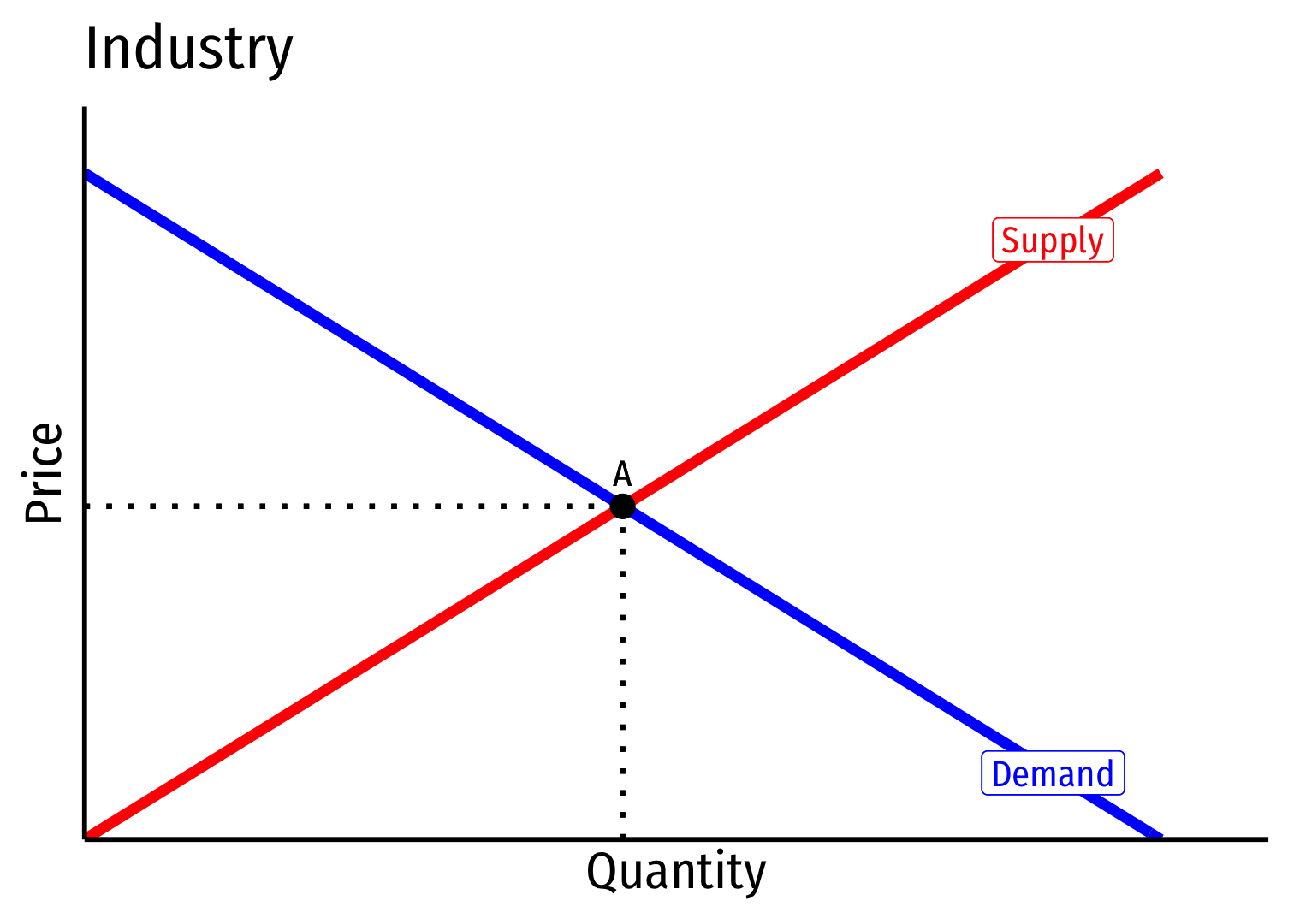
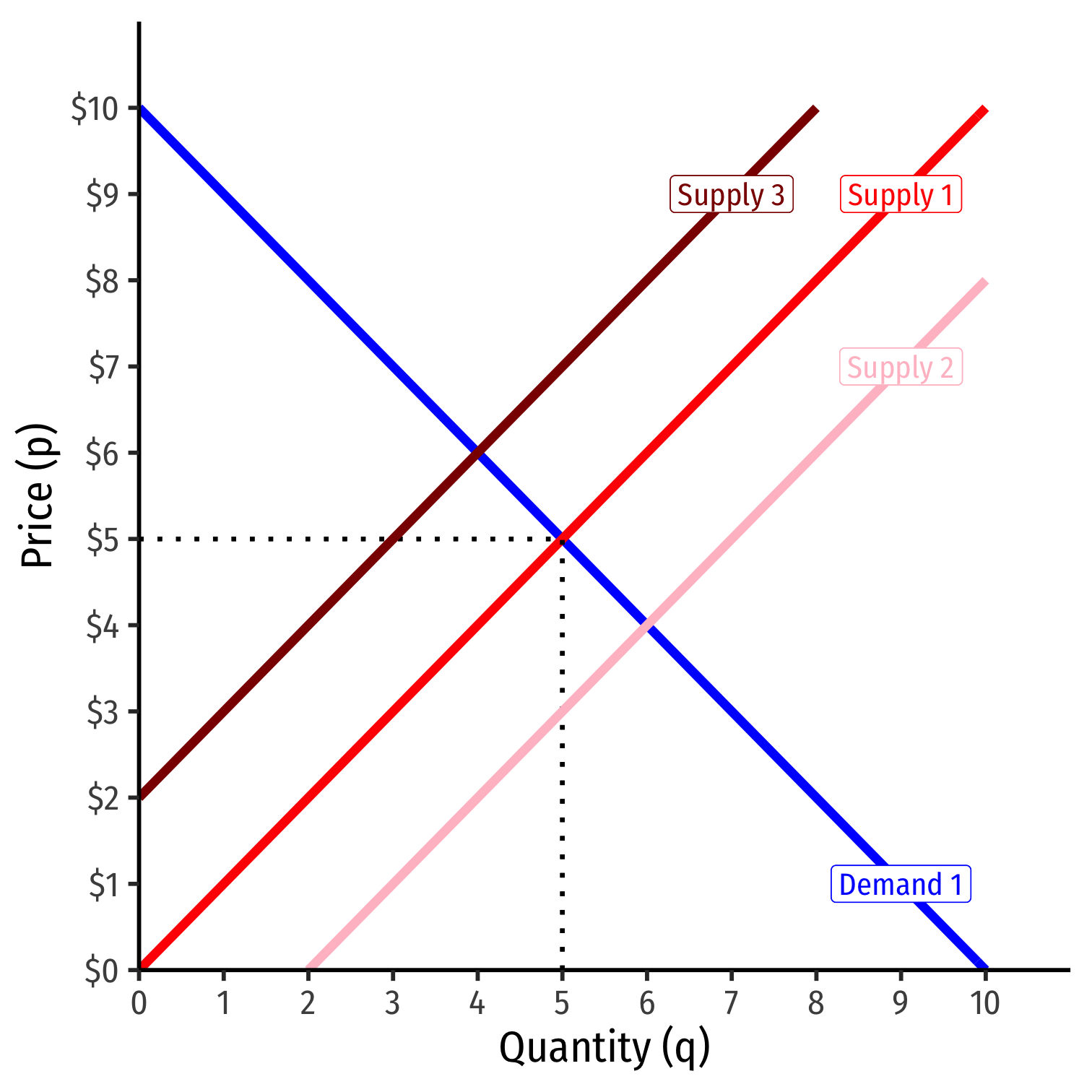
- Industry equilibrium: firms earning normal \(\color{#047806}{\pi=0}, \color{blue}{p}=\color{red}{MC(q)}=\color{orange}{AC(q)}\) at points a, A
Constant Cost Industry (No External Economies) III
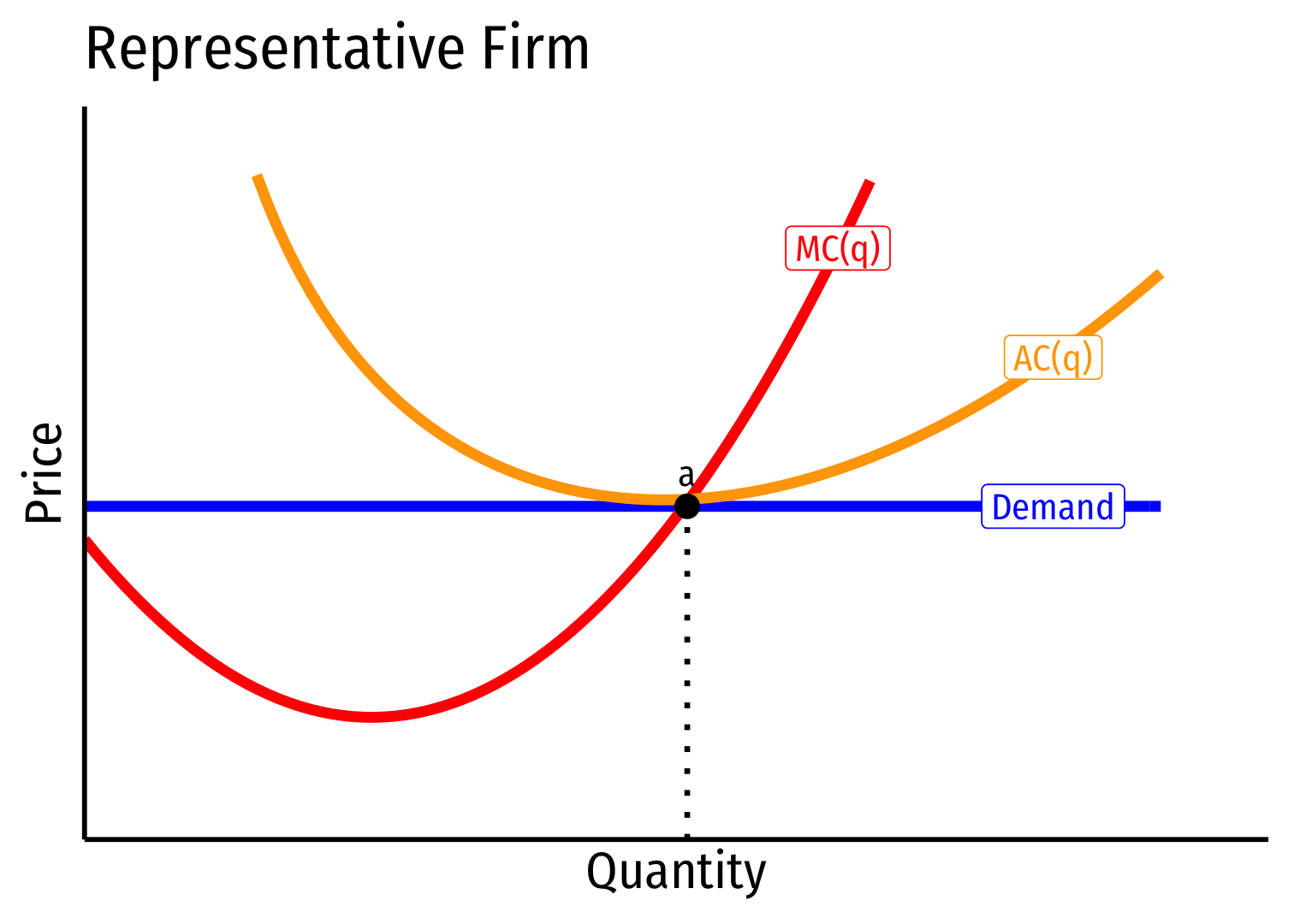
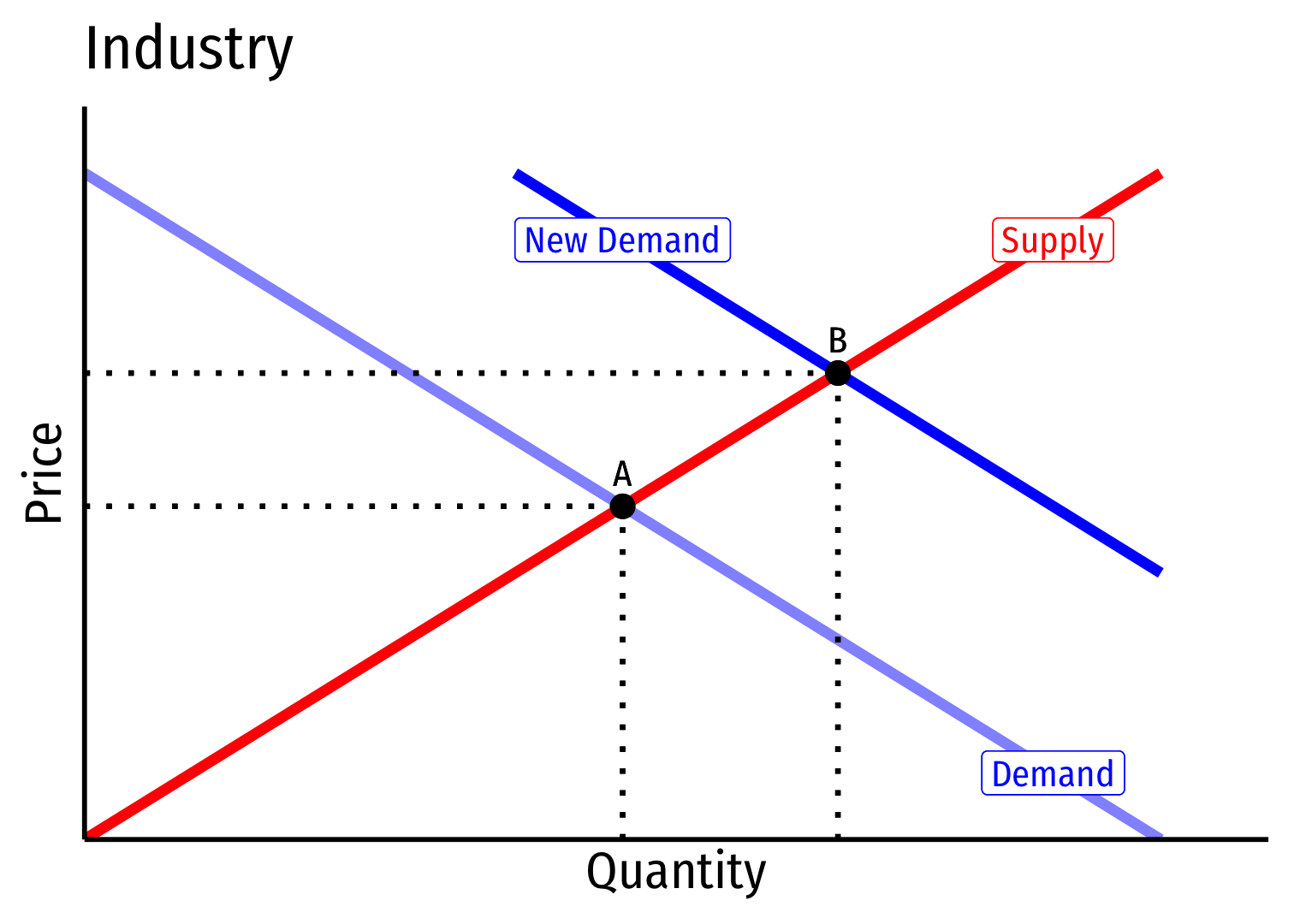
Industry equilibrium: firms earning normal \(\color{#047806}{\pi=0}, \color{blue}{p}=\color{red}{MC(q)}=\color{orange}{AC(q)}\) at points a, A
Consider an increase in market demand
Constant Cost Industry (No External Economies) IV
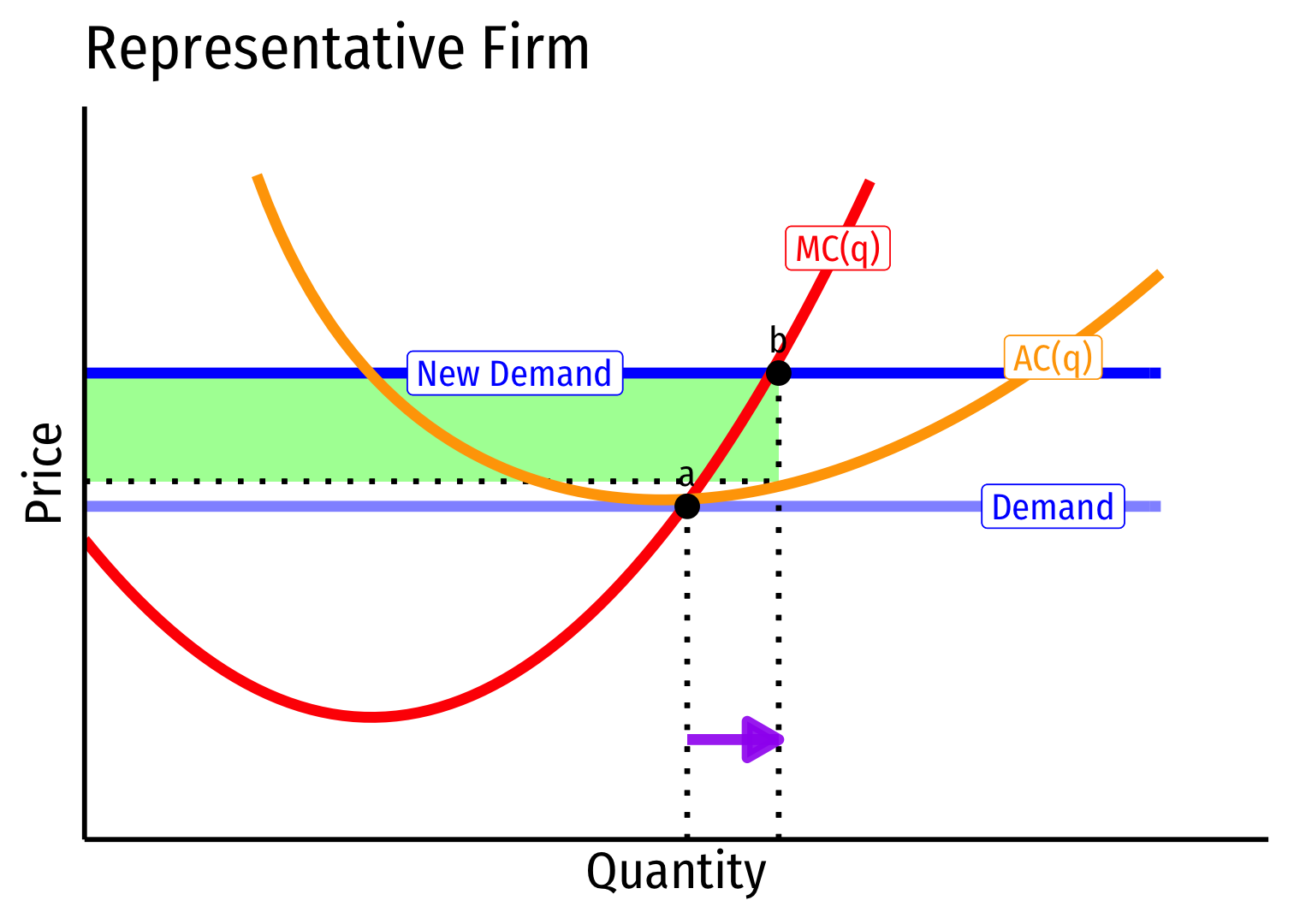

Short run \((A \rightarrow B)\): industry reaches new equilibrium at higher price
Firms charge higher price, produce more output, earn \(\color{#047806}{\pi}\) at point b
Constant Cost Industry (No External Economies) V
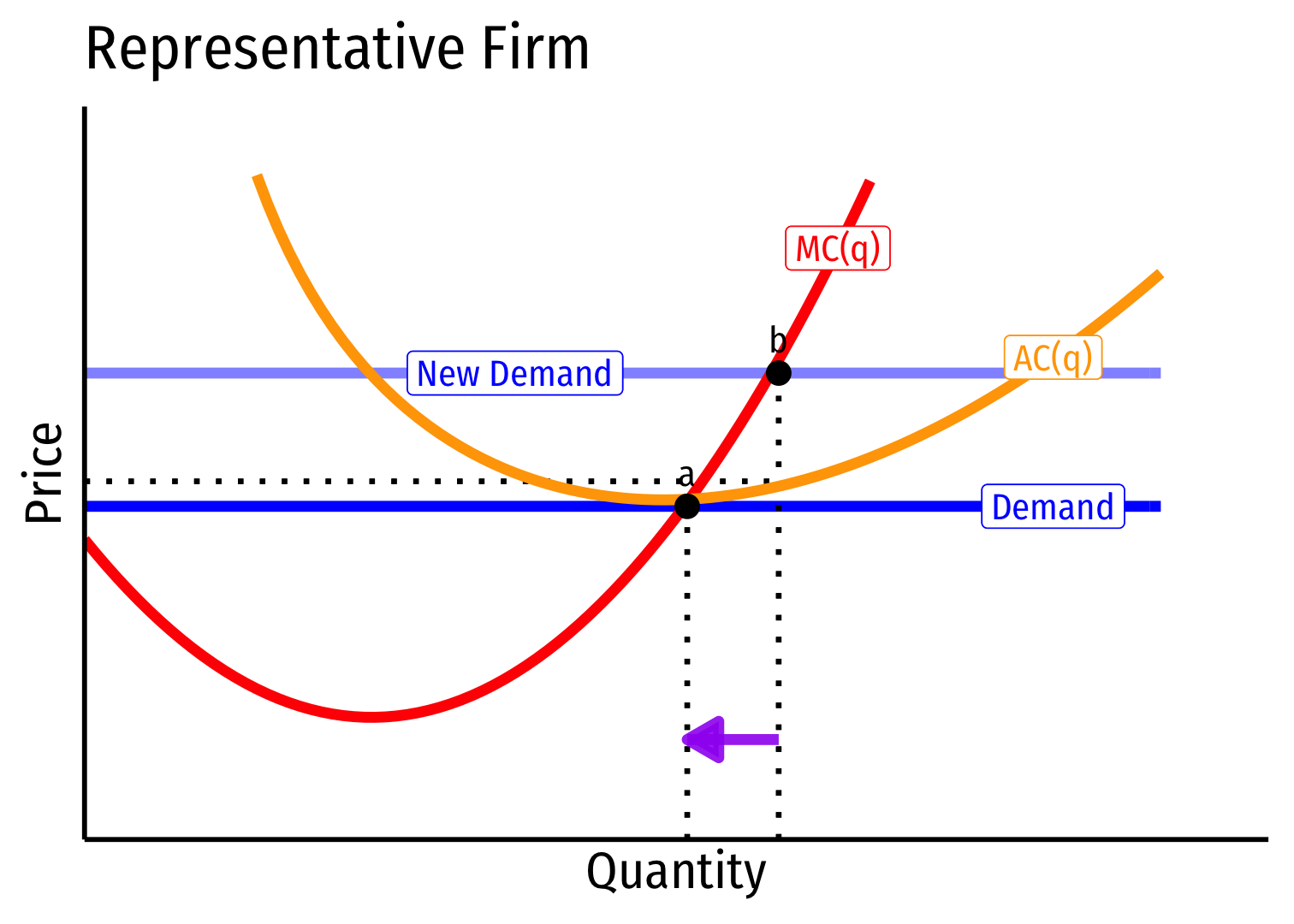

Long run \((B \rightarrow C)\): profit attracts entry \(\implies\) industry supply increases (pushing down price)
No change in costs to firms in industry, new firms continue to enter until \(\color{#047806}{\pi=0}\) at \(\color{blue}{p}=\color{orange}{AC(q)}\) for firms
Firms return to point a, original price, output, and \(\color{#047806}{\pi=0}\)
Constant Cost Industry (No External Economies) VI
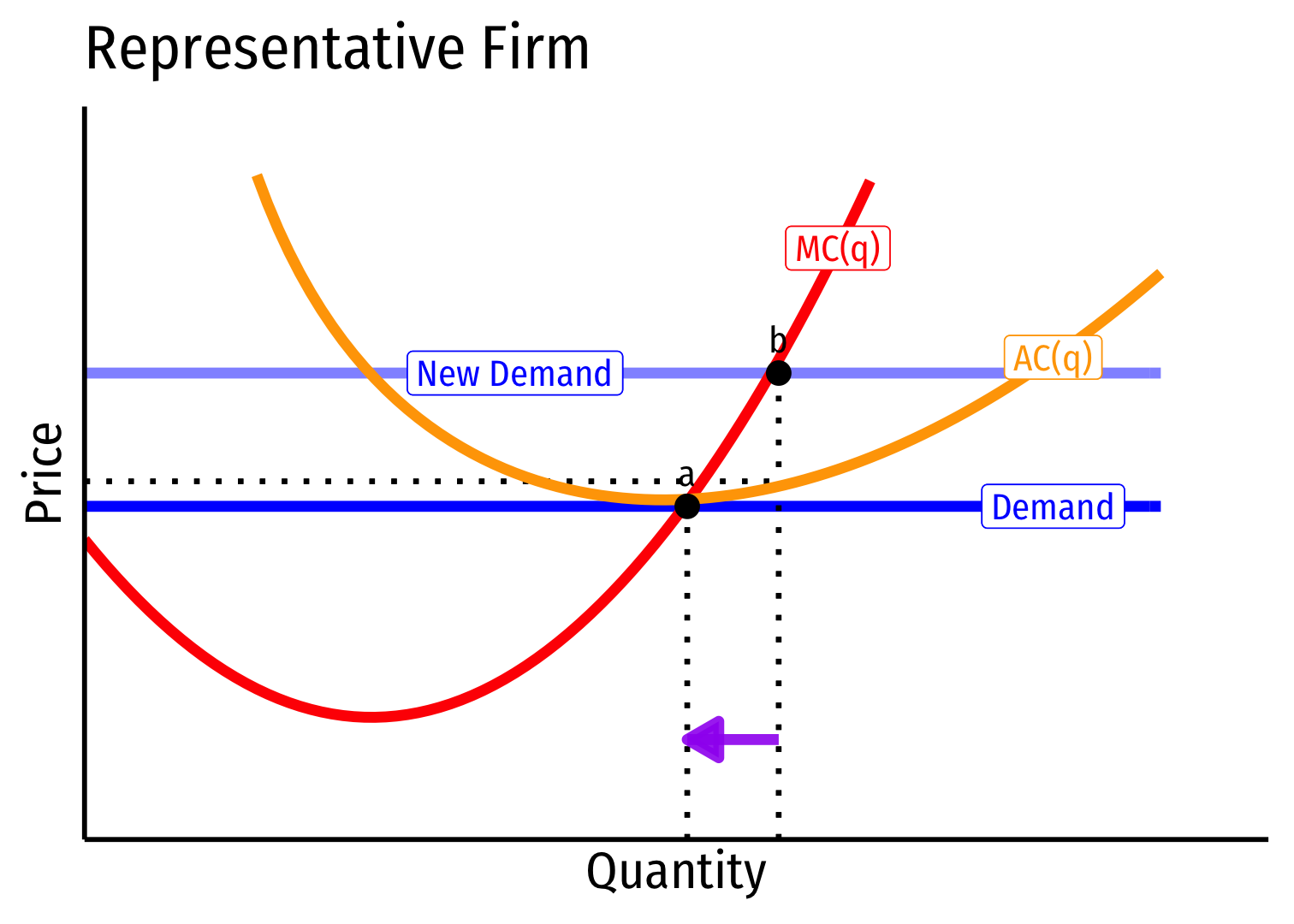
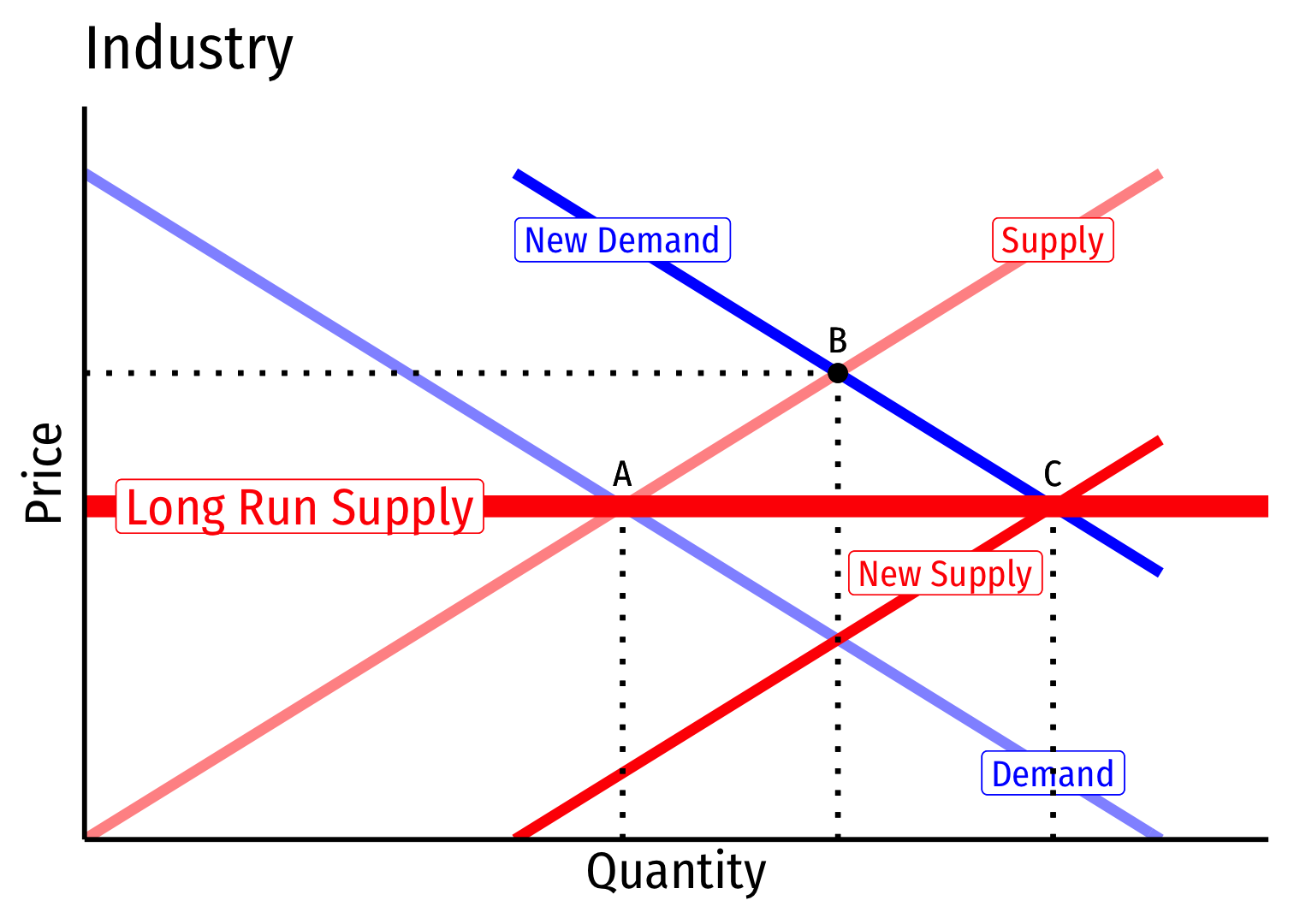
- Long Run Industry Supply is perfectly elastic
- Long run price is not affected in any way by Market Demand!
Increasing Cost Industry (External Diseconomies) I
Increasing cost industry has external diseconomies, costs rise for all firms in the industry as industry output increases (firms enter & incumbents produce more)
An upward sloping long-run industry supply curve
Determinants:
- Finding more resources in harder-to-reach places
- Diminishing marginal products
- Greater complexity and administrative costs at larger scales
Examples: oil, mining, particle physics


Increasing Cost Industry (External Diseconomies) II
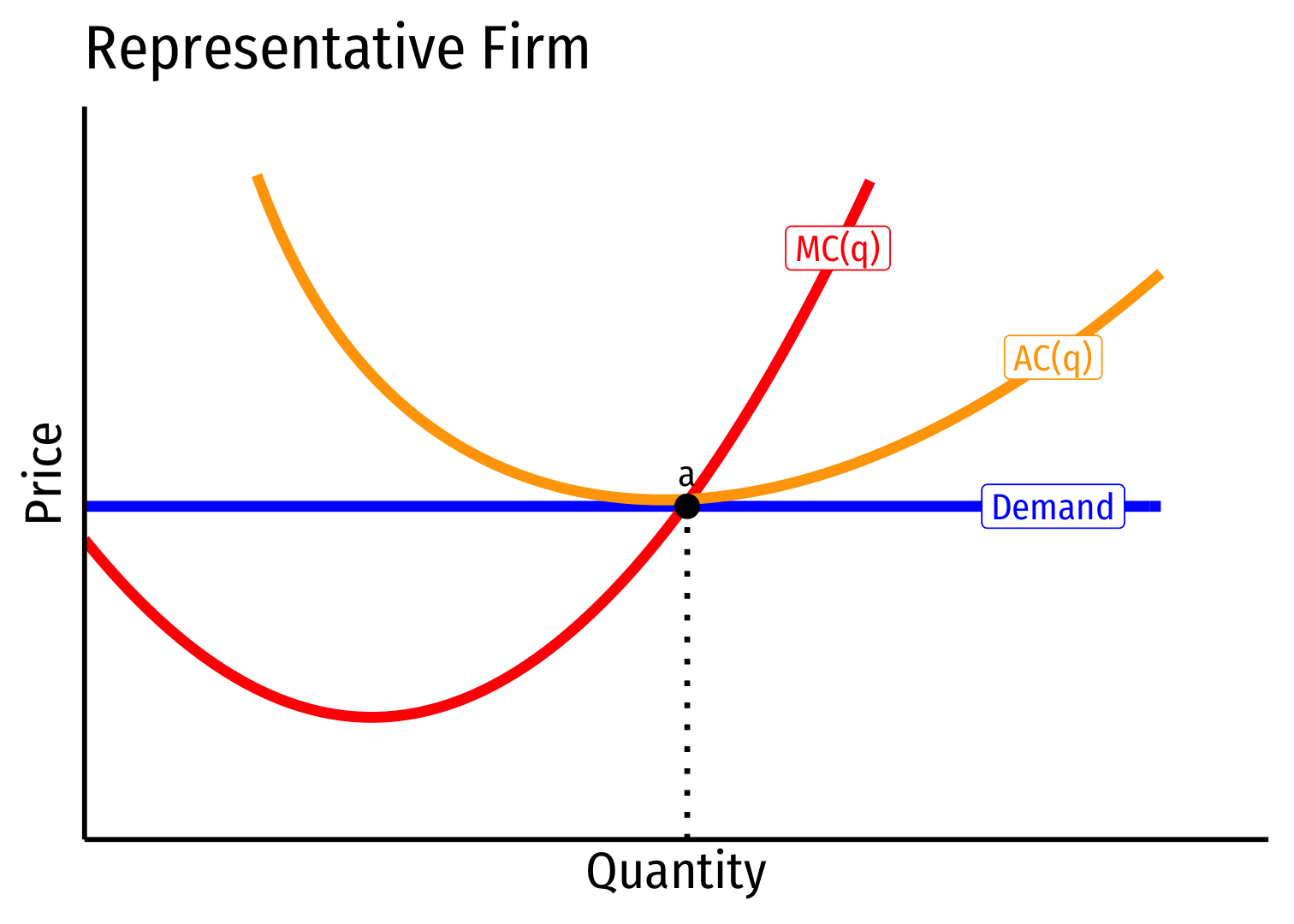

- Industry equilibrium: firms earning normal \(\pi=0, p=MC(q)=AC(q)\)
Increasing Cost Industry (External Diseconomies) III
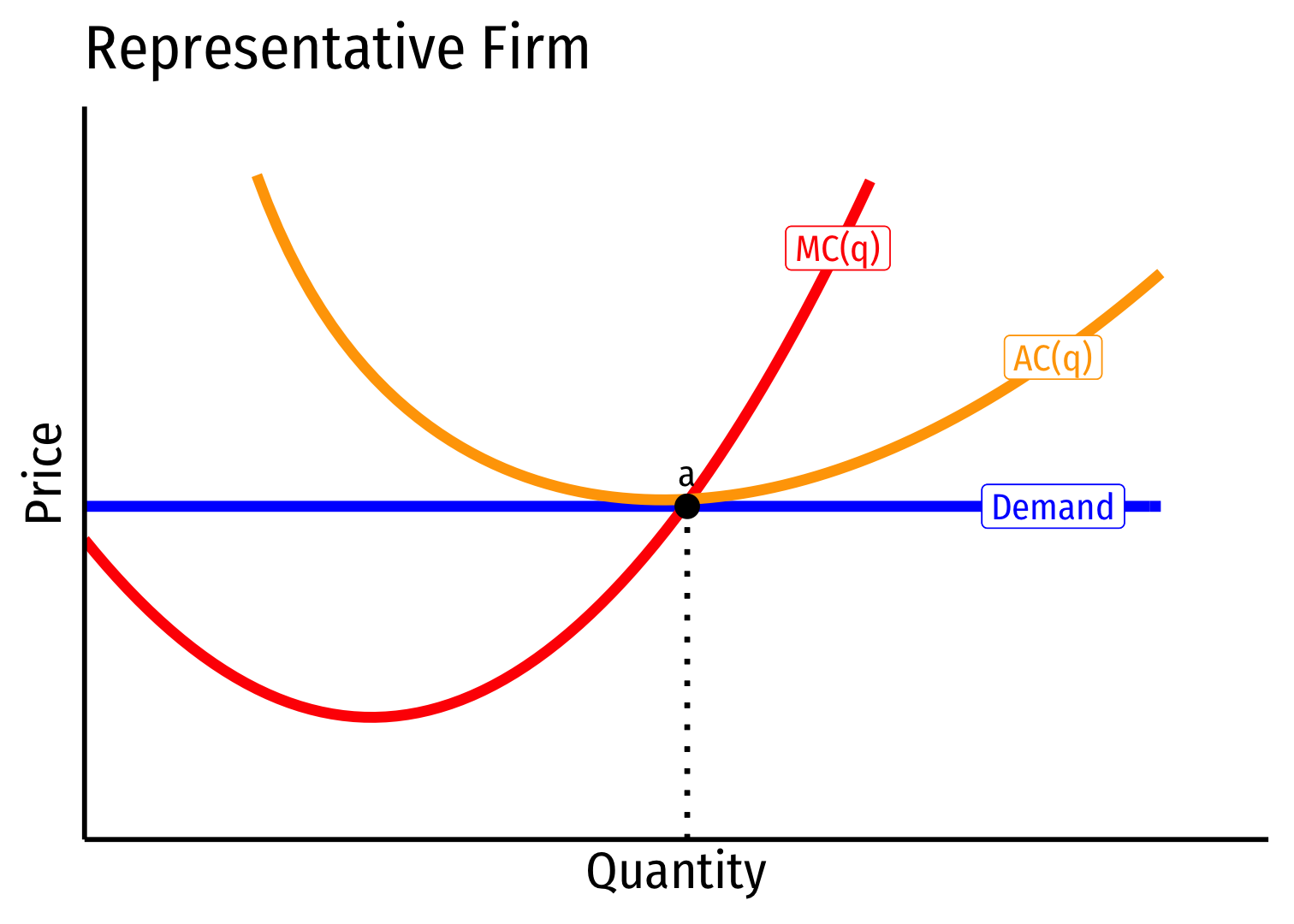
Industry equilibrium: firms earning normal \(\pi=0, p=MC(q)=AC(q)\)
Exogenous increase in market demand
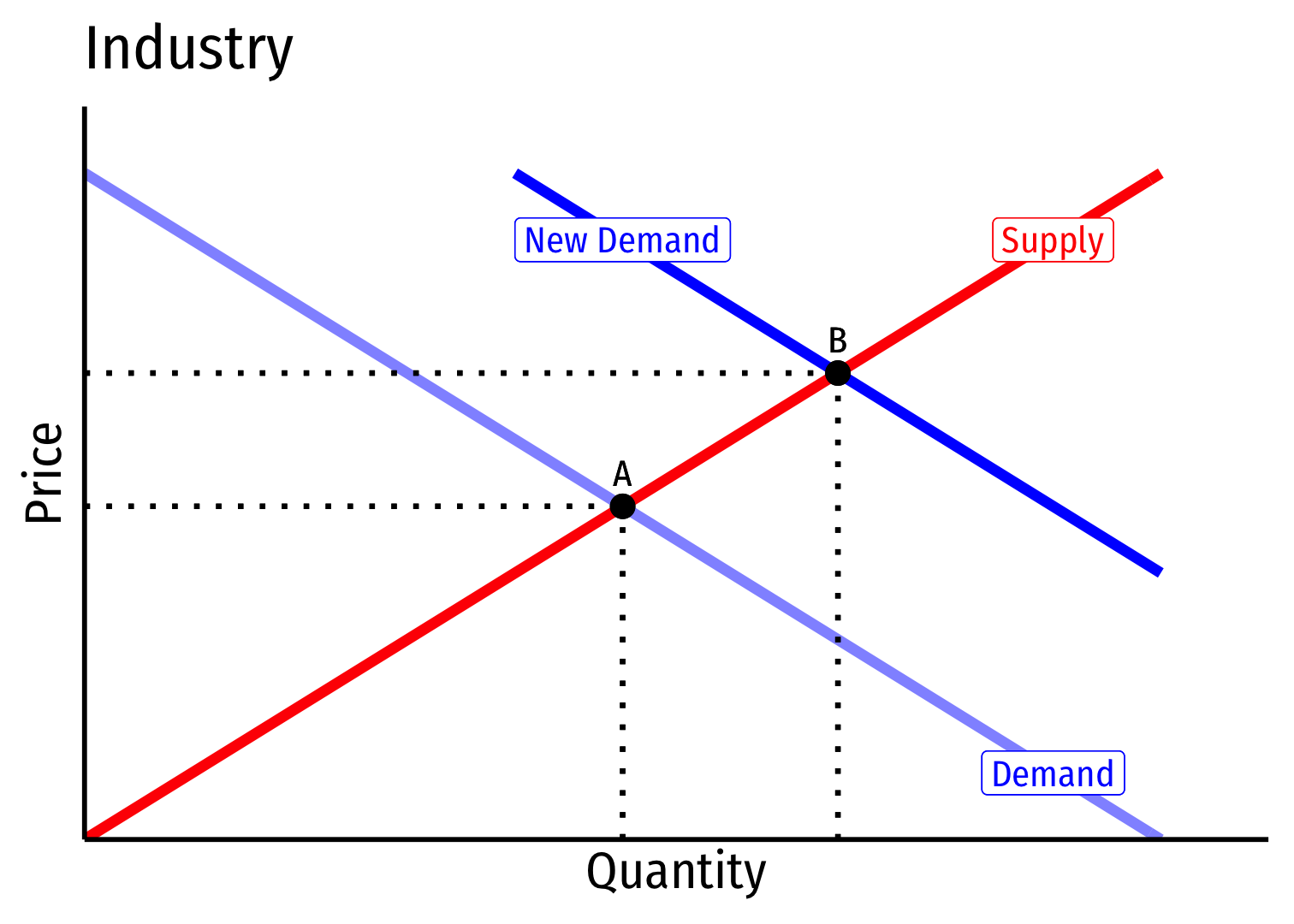
Increasing Cost Industry (External Diseconomies) IV
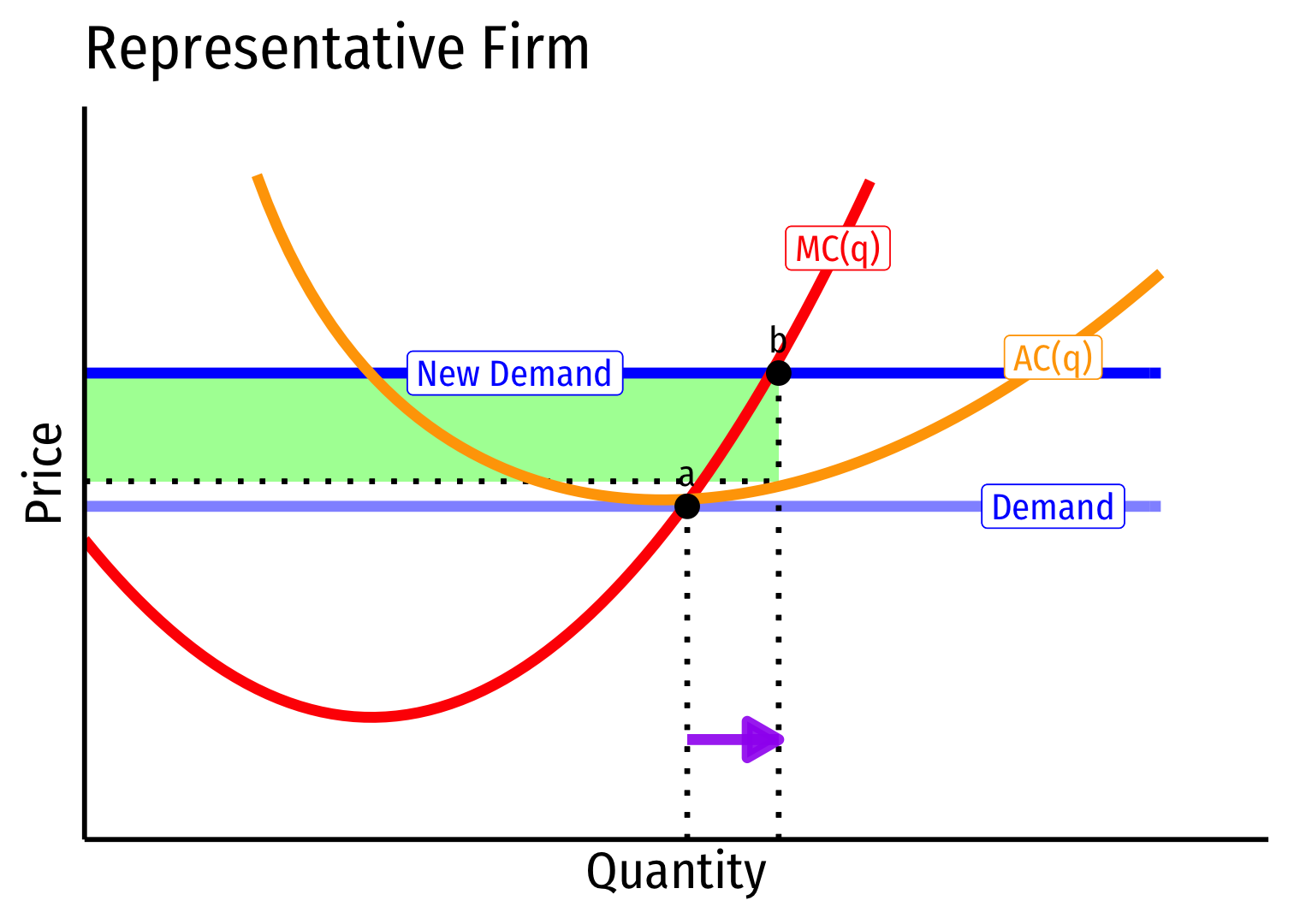
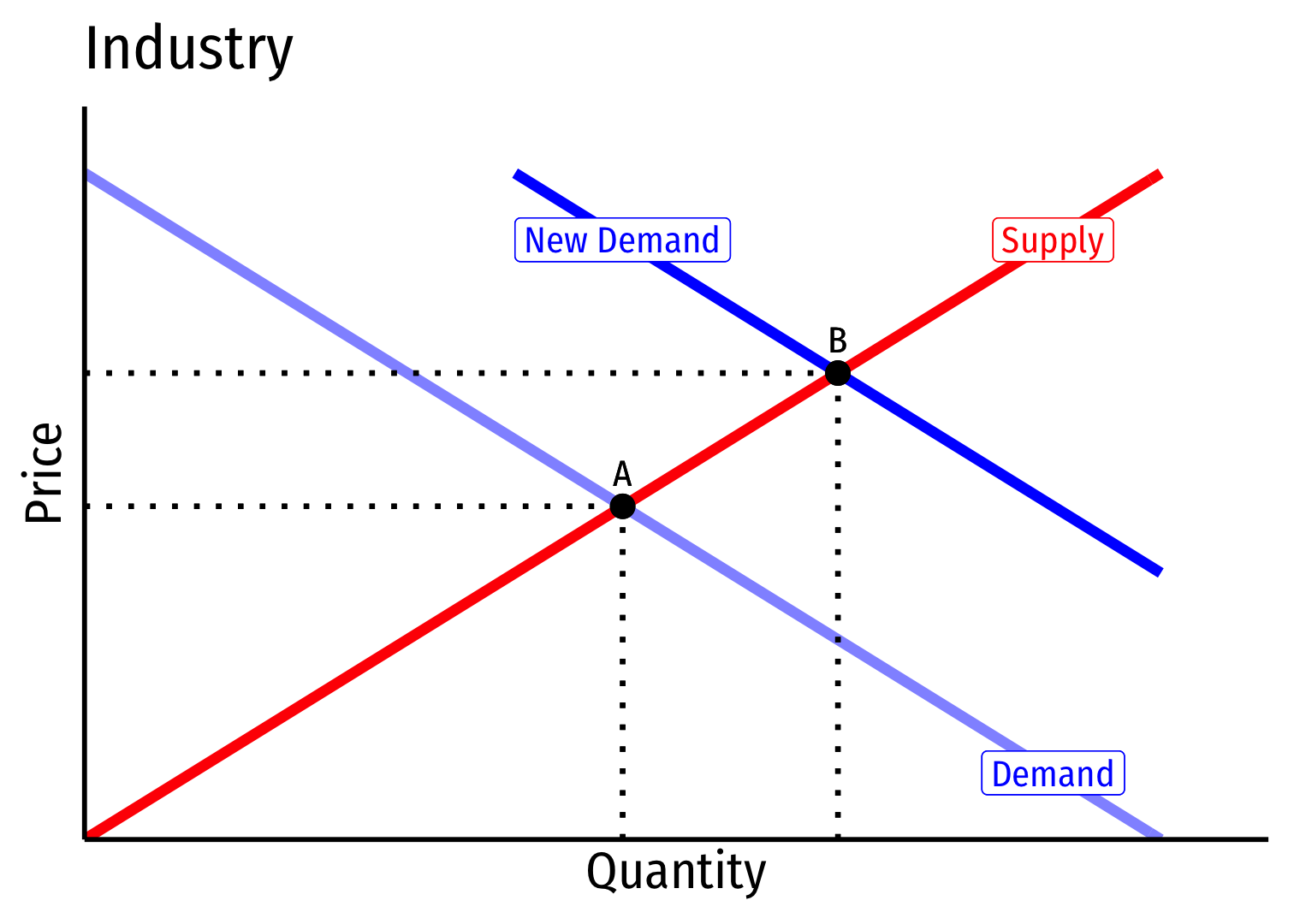
Short run \((A \rightarrow B)\): industry reaches new equilibrium
Firms charge higher \(p^*\), produce more \(q^*\), earn \(\pi\)
Increasing Cost Industry (External Diseconomies) V
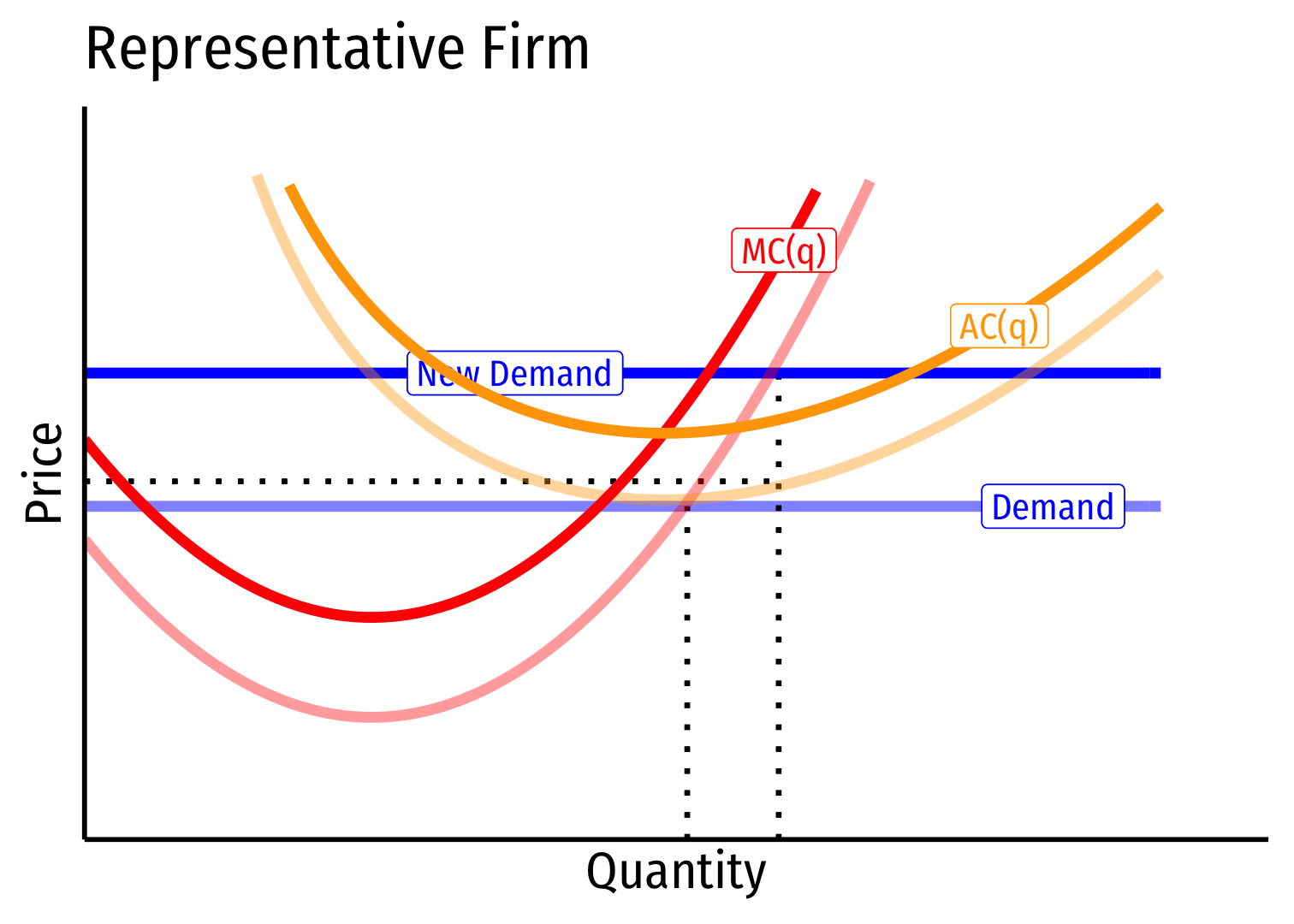
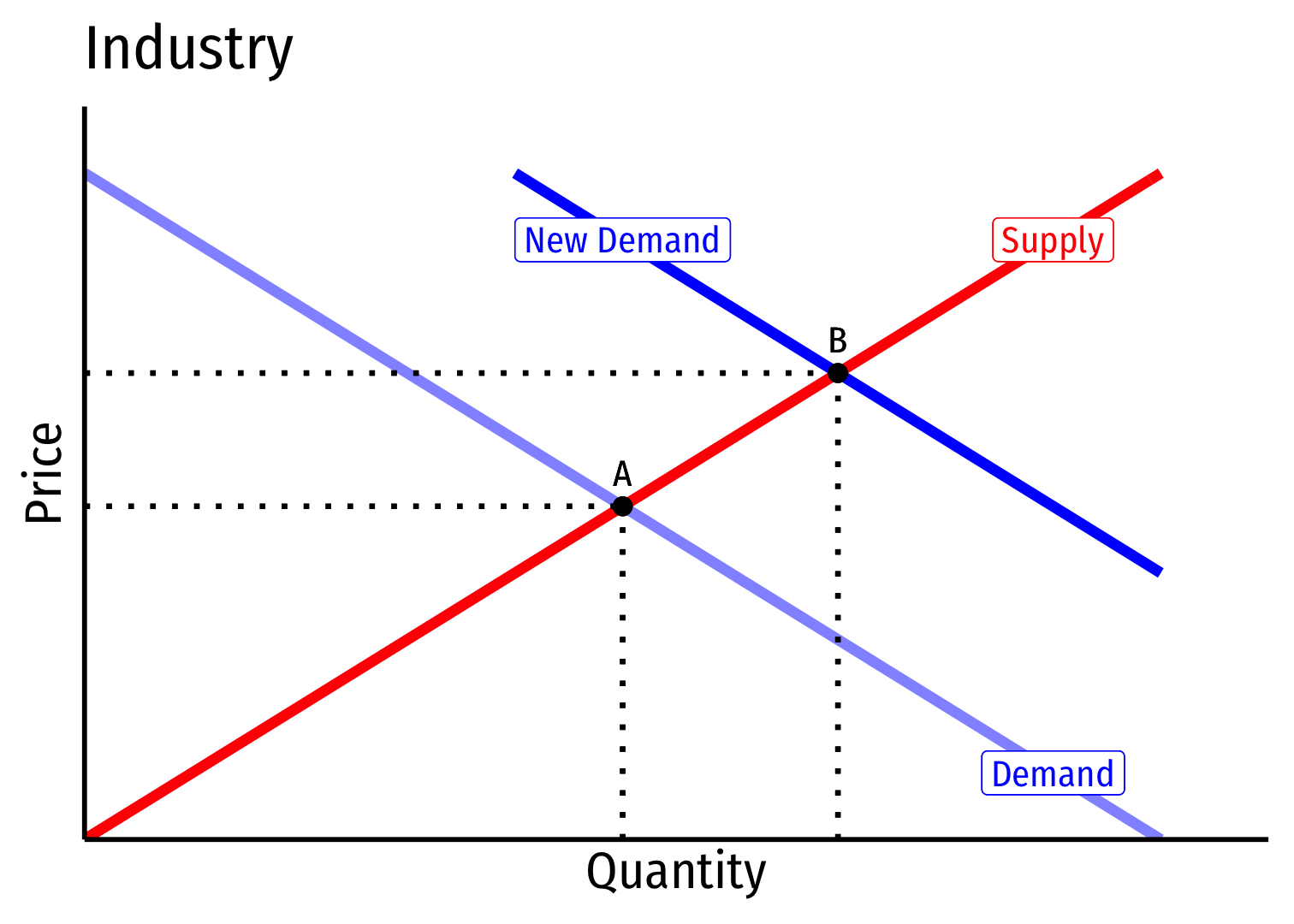
Long run: profit attracts entry \(\implies\) industry supply will increase
But more industry-wide output increases costs (MC(q), AC(q)) for all firms in industry
Increasing Cost Industry (External Diseconomies) VI
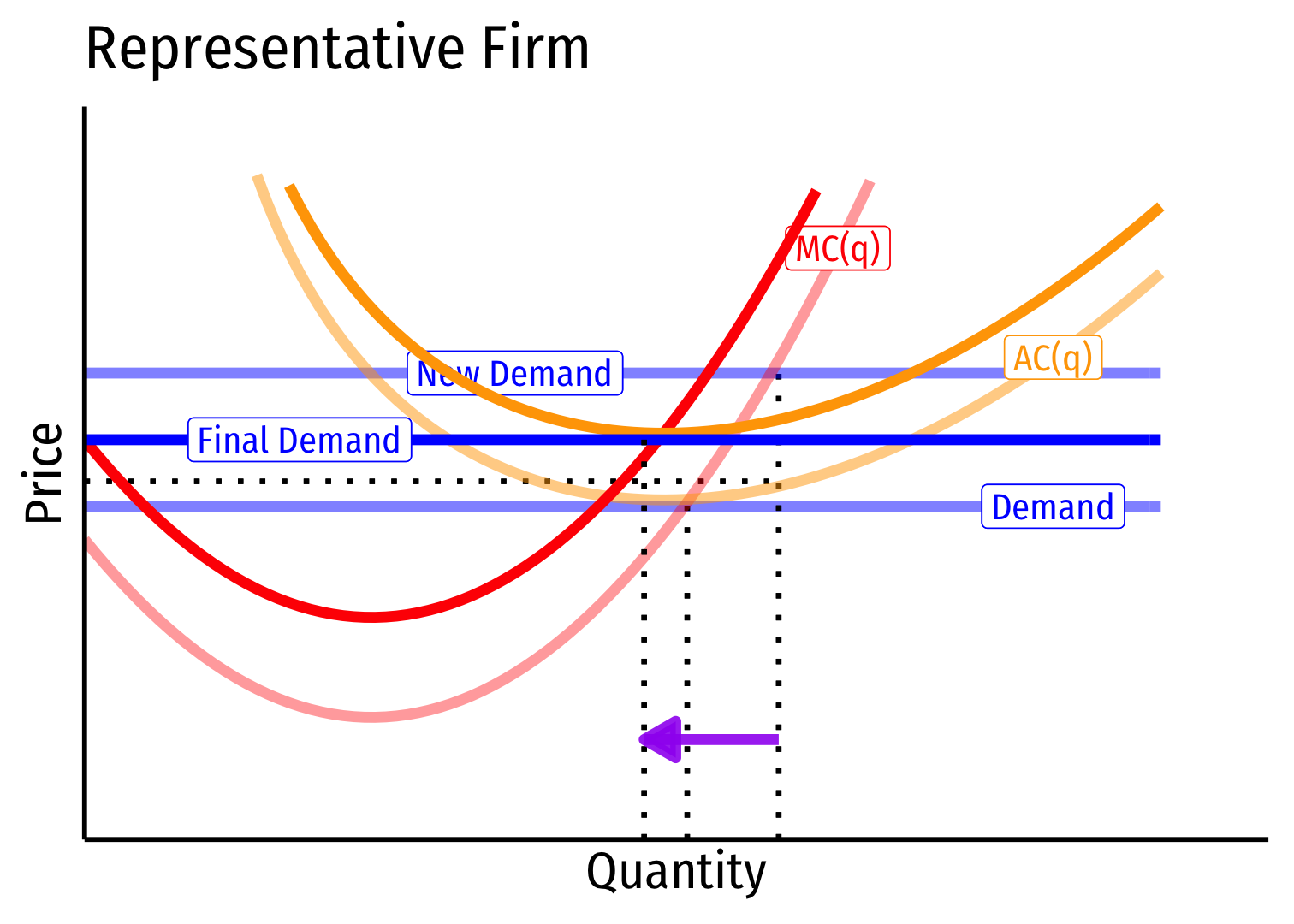
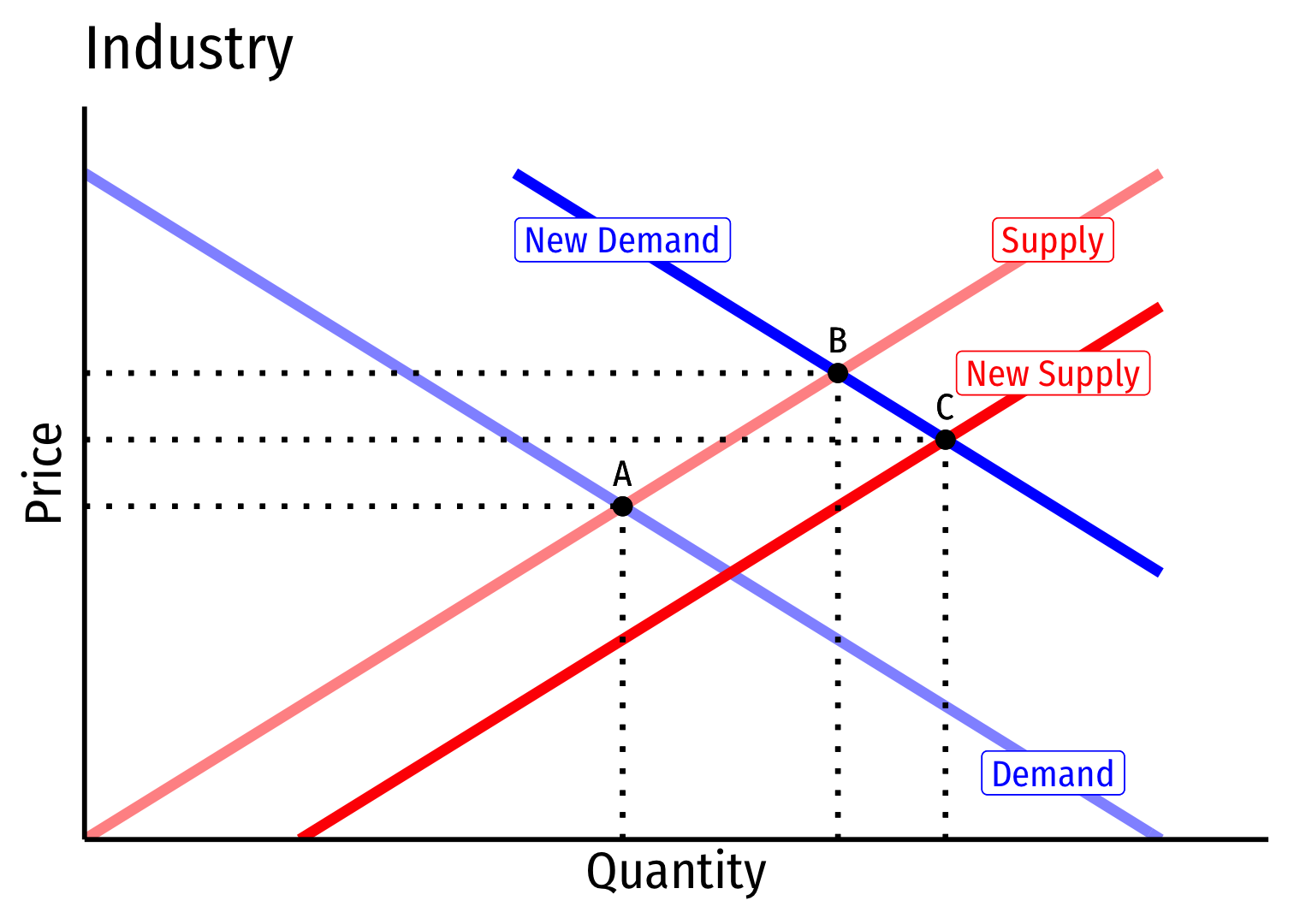
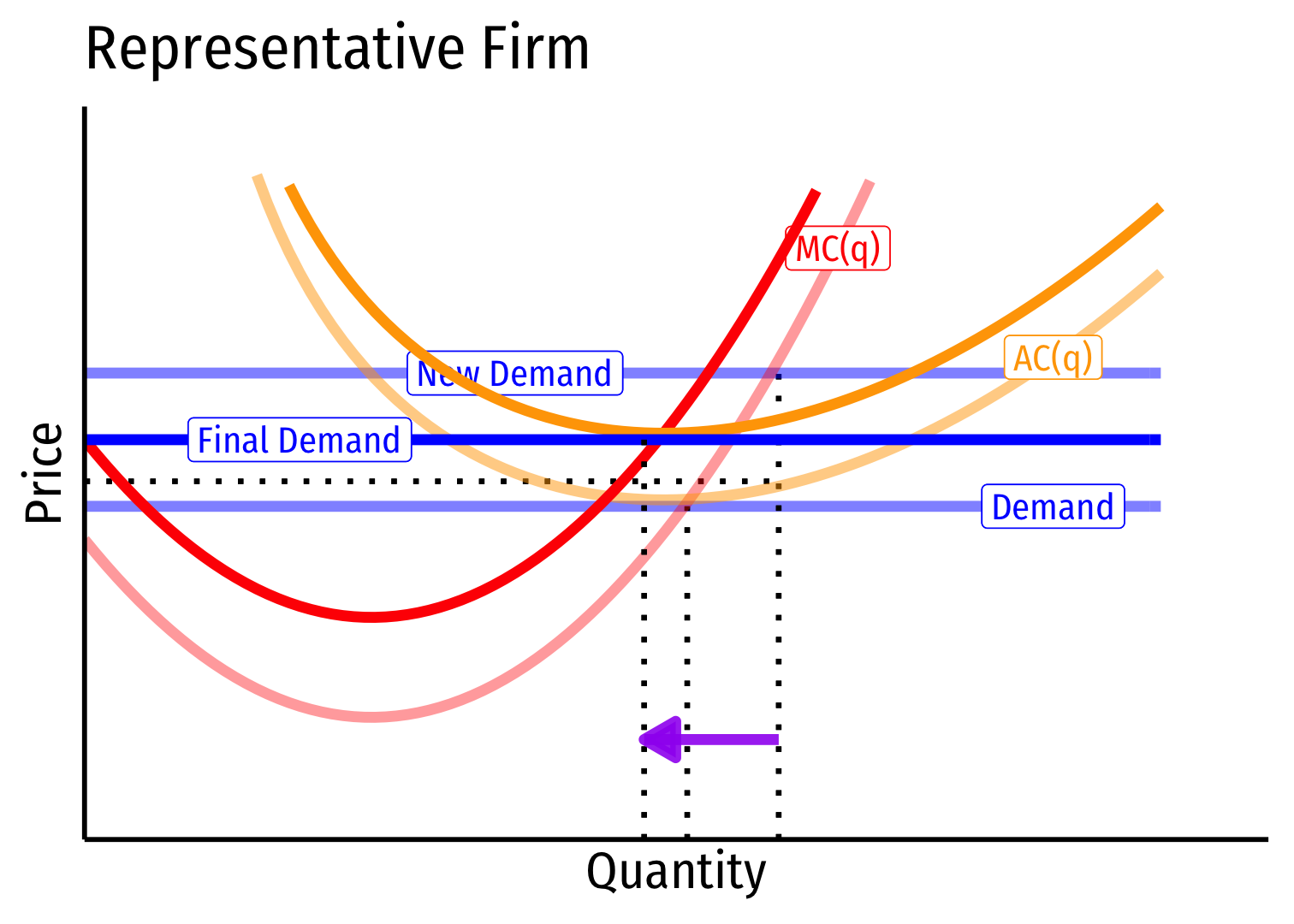
Long run \((B \rightarrow C)\): firms enter until \(\pi=0\) at \(p=AC(q)\)
Firms charge higher \(p^*\), producer lower \(q^*\), earn \(\pi=0\)
Increasing Cost Industry (External Diseconomies) VII
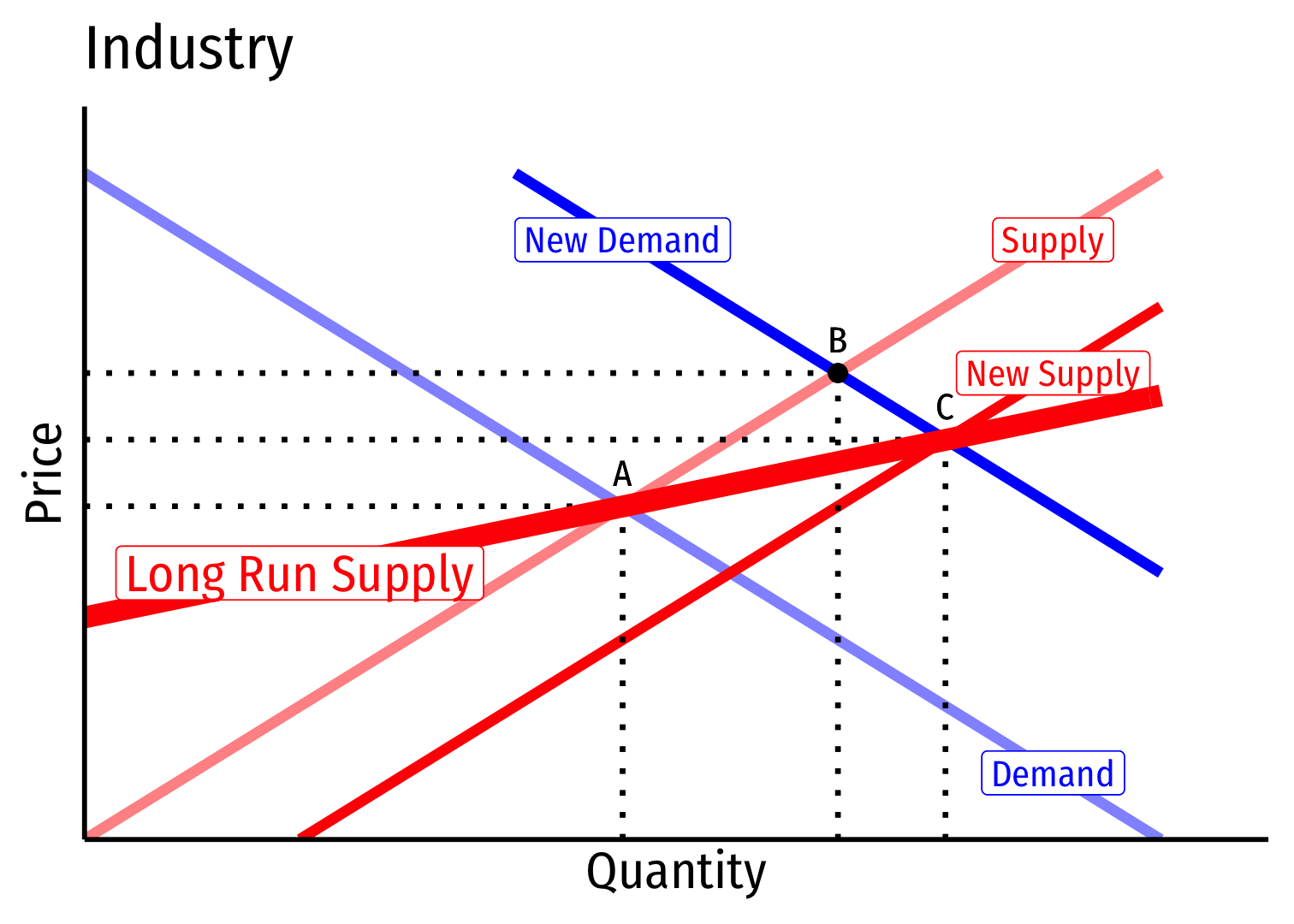
- Long run industry supply curve is upward sloping
Decreasing Cost Industry (External Economies) I
Decreasing cost industry has external economies, costs fall for all firms in the industry as industry output increases (firms enter & incumbents produce more)
A downward sloping long-run industry supply curve!
Determinants:
- High fixed costs, low marginal costs
- Economies of scale
Examples: geographic clusters, public utilities, infrastructure, entertainment
Tends towards "natural" monopoly


Decreasing Cost Industry (External Economies) II
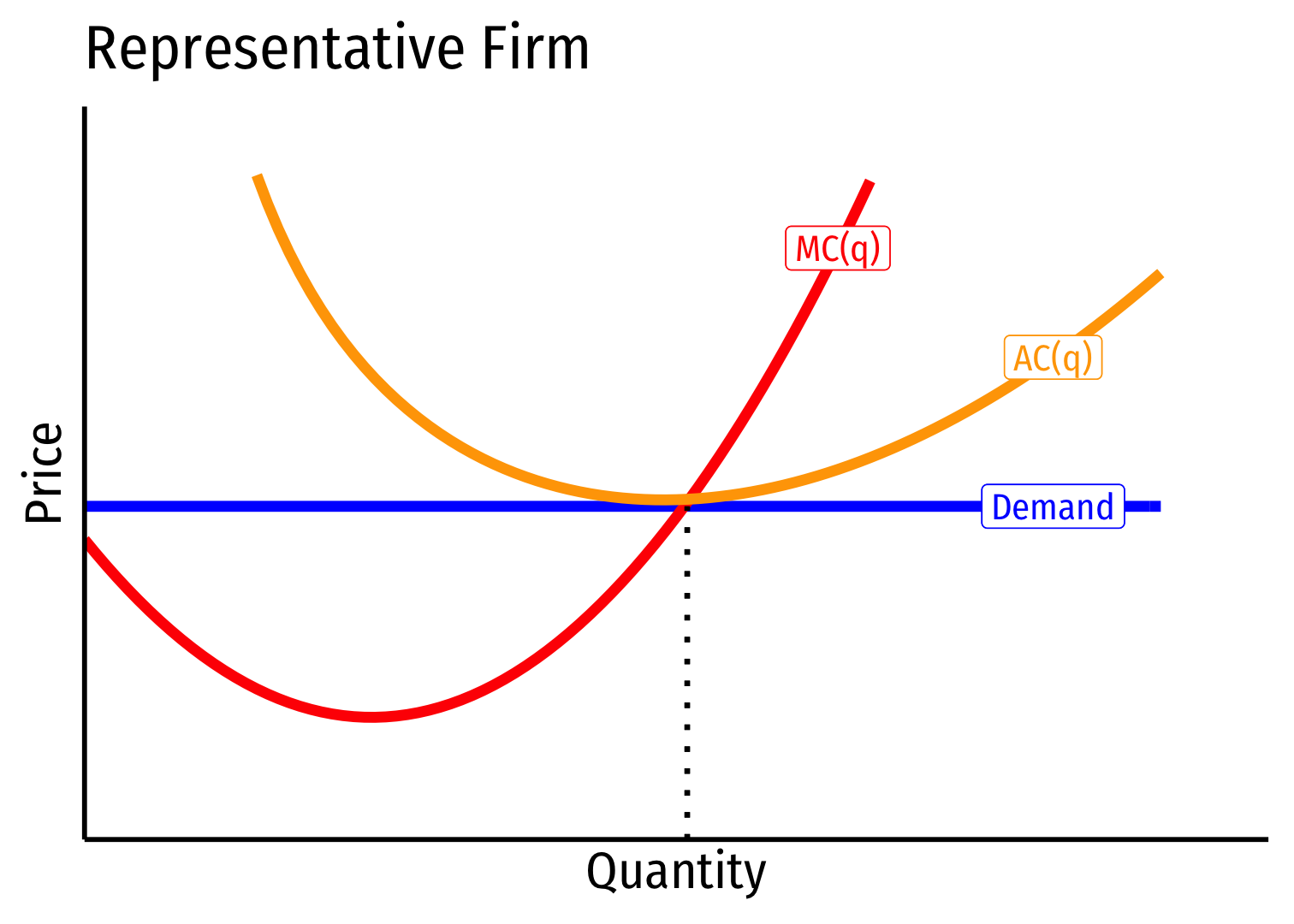
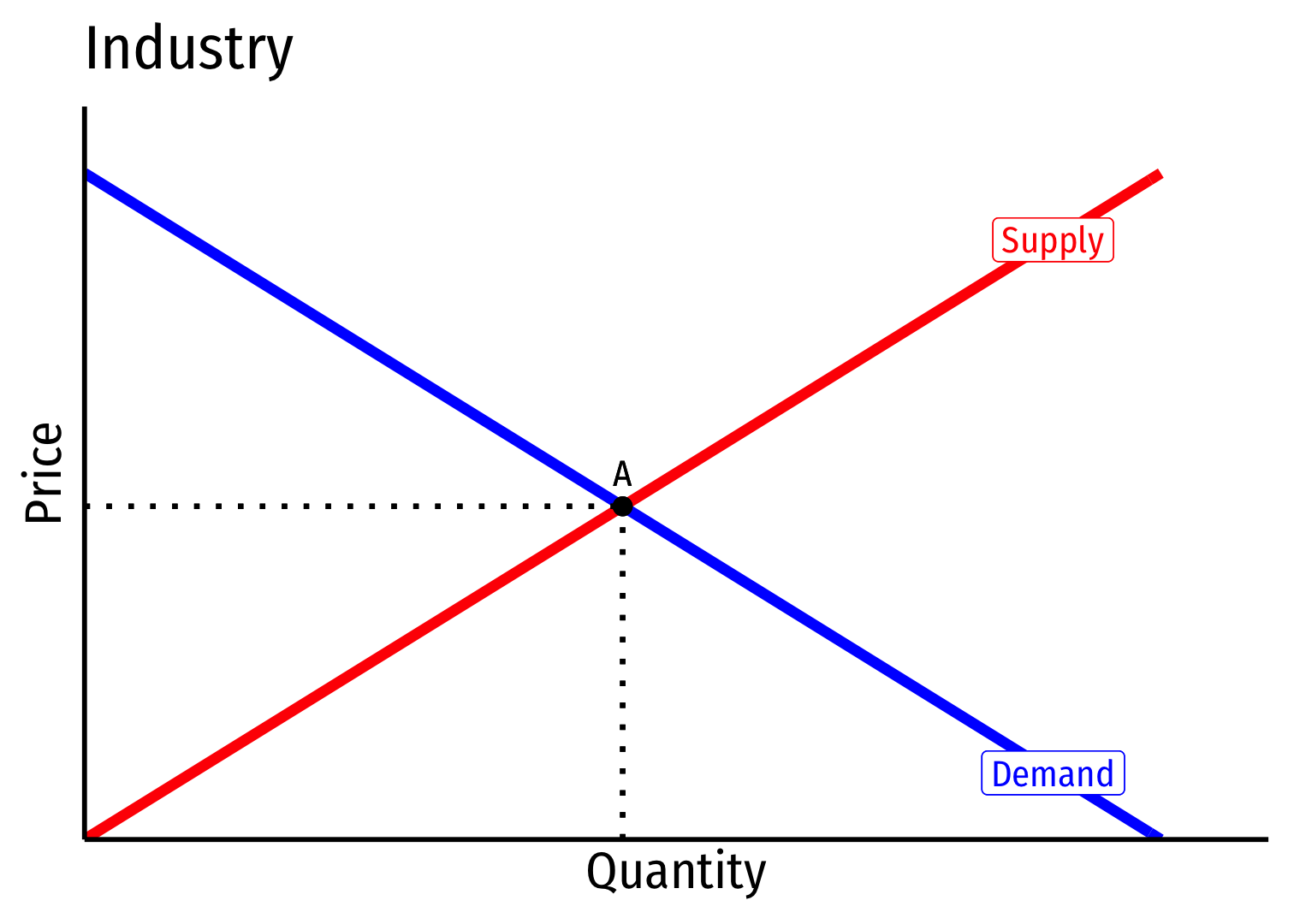
- Industry equilibrium: firms earning normal \(\pi=0, p=MC(q)=AC(q)\)
Decreasing Cost Industry (External Economies) III
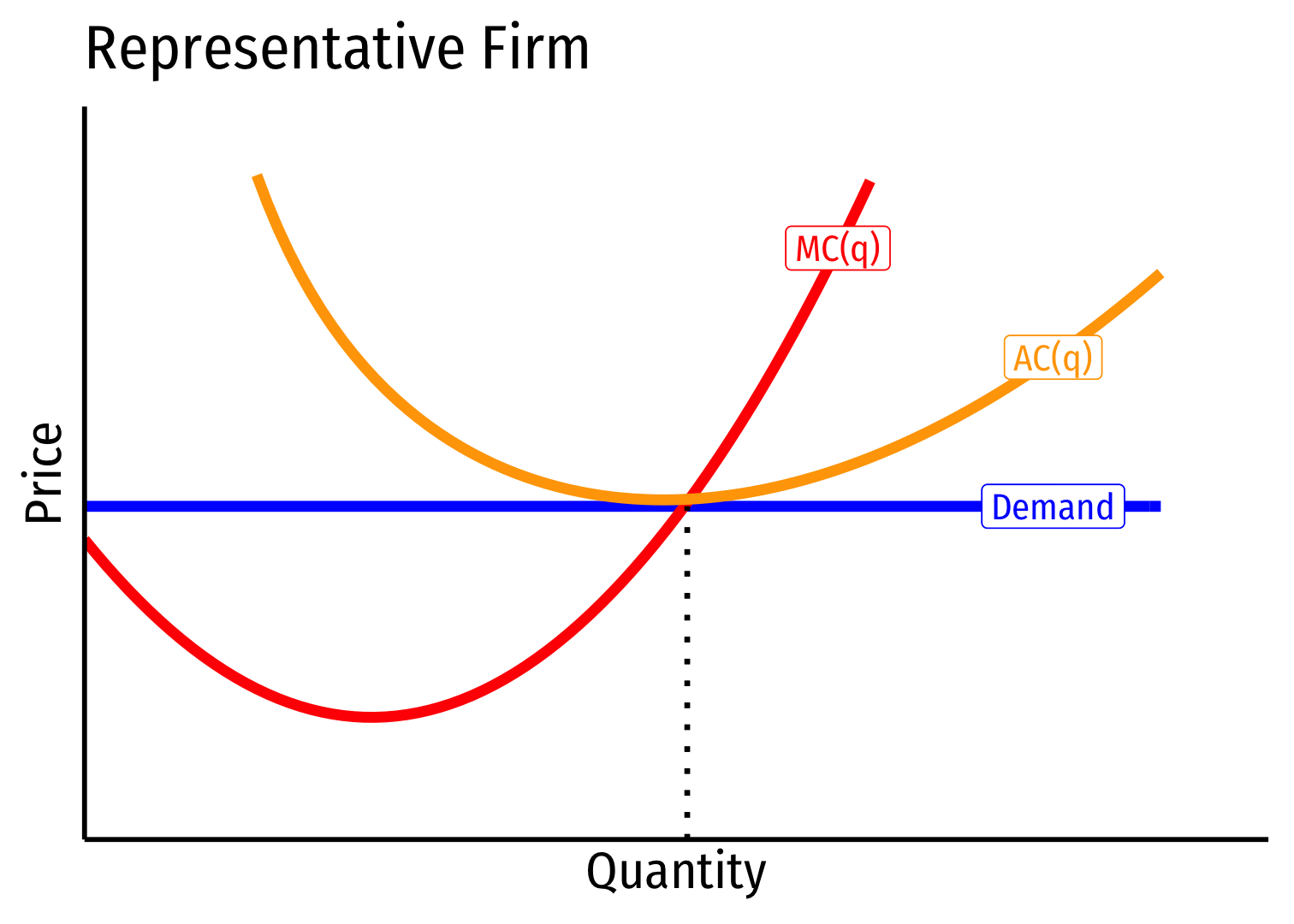
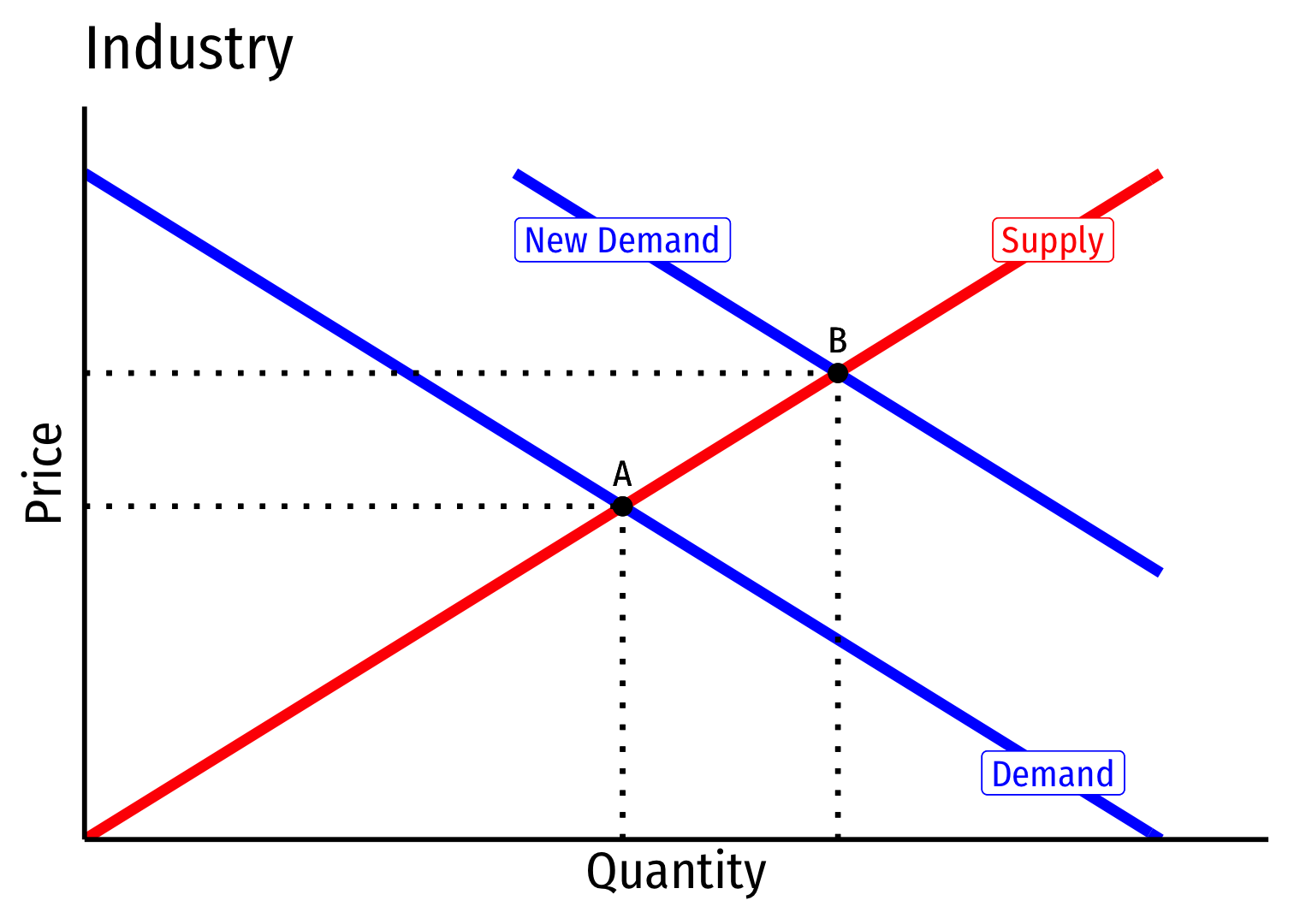
Industry equilibrium: firms earning normal \(\pi=0, p=MC(q)=AC(q)\)
Exogenous increase in market demand
Decreasing Cost Industry (External Economies) IV
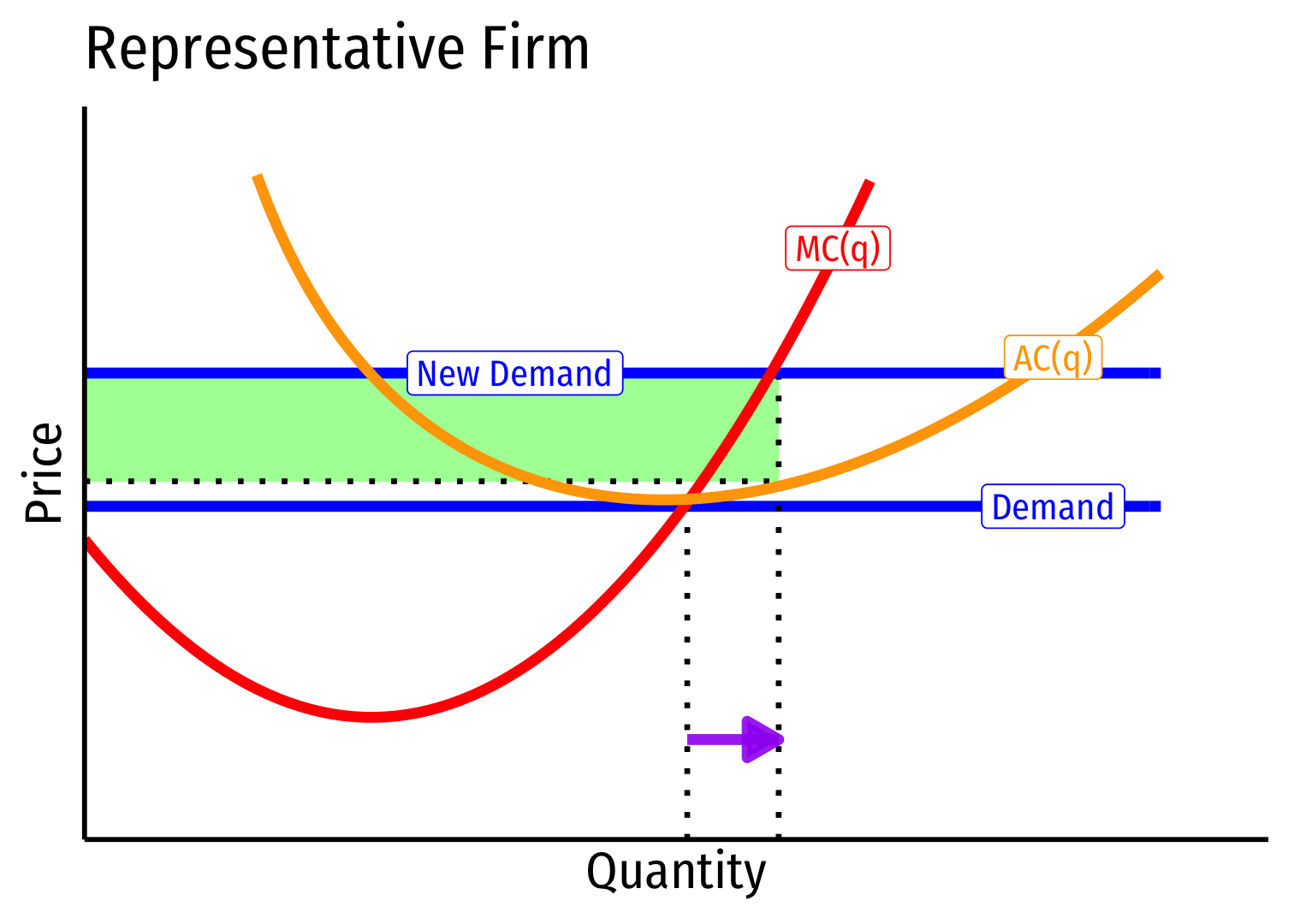
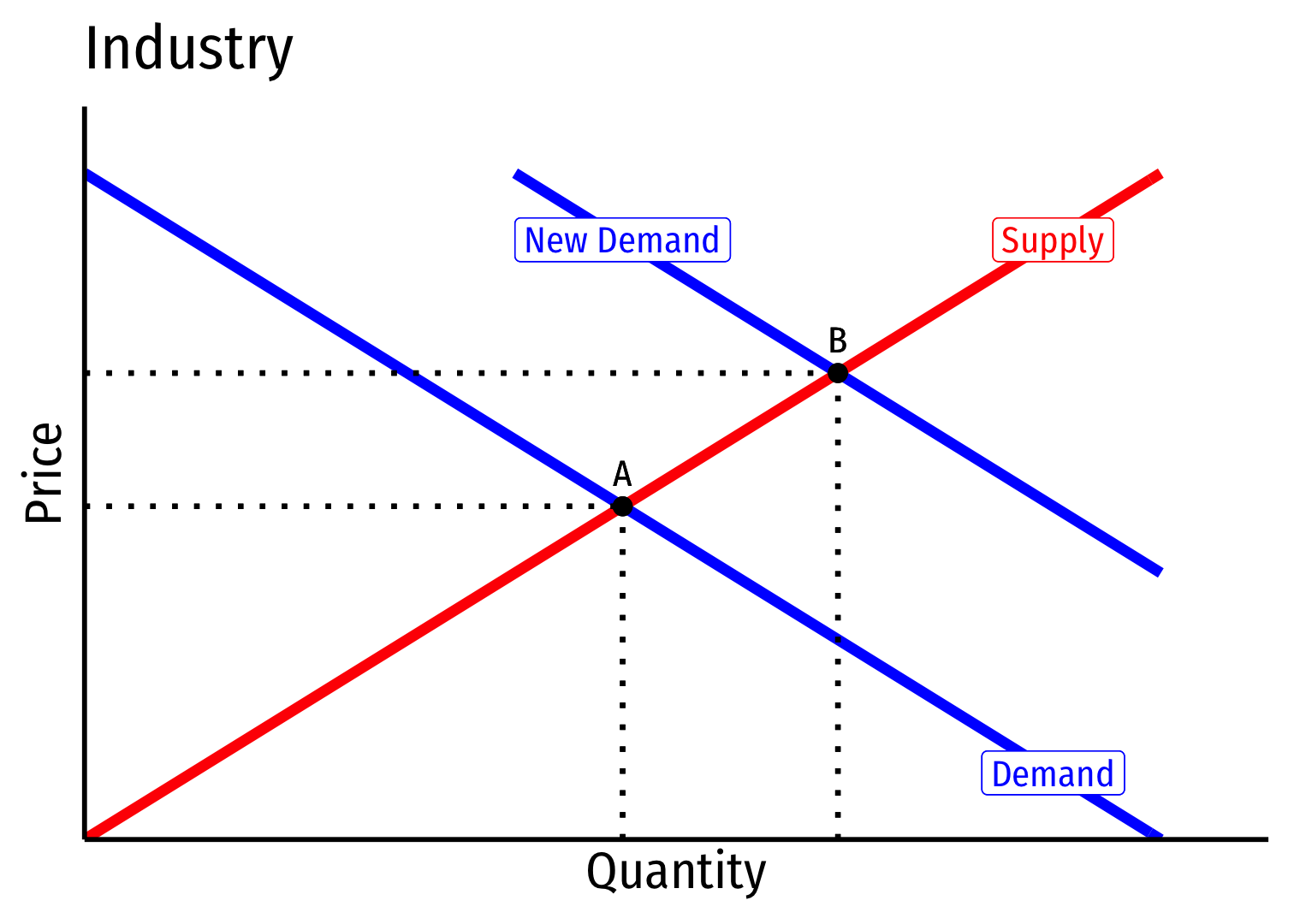
Short run \((A \rightarrow B)\): industry reaches new equilibrium
Firms charge higher \(p^*\), produce more \(q^*\), earn \(\pi\)
Decreasing Cost Industry (External Economies) V
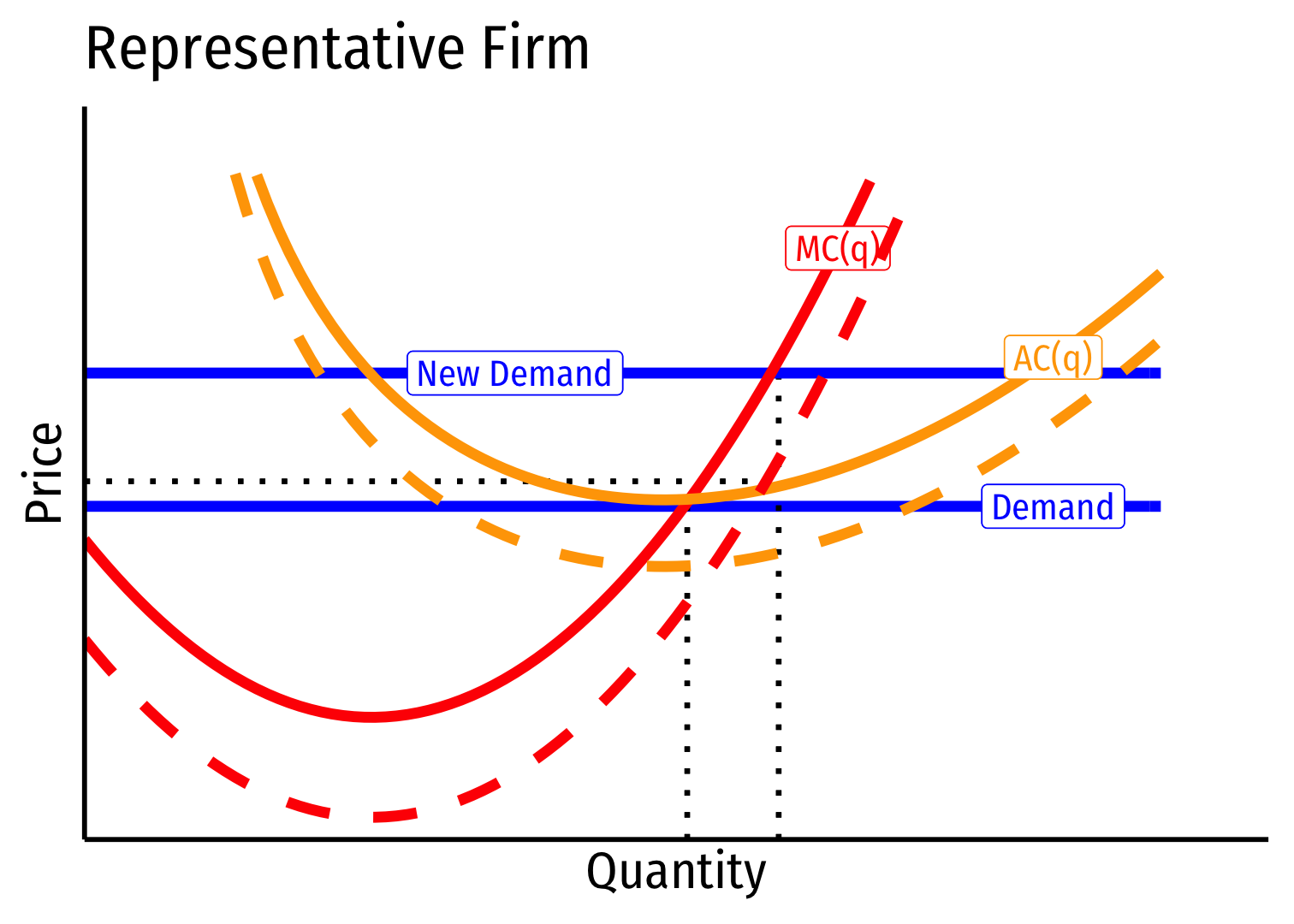
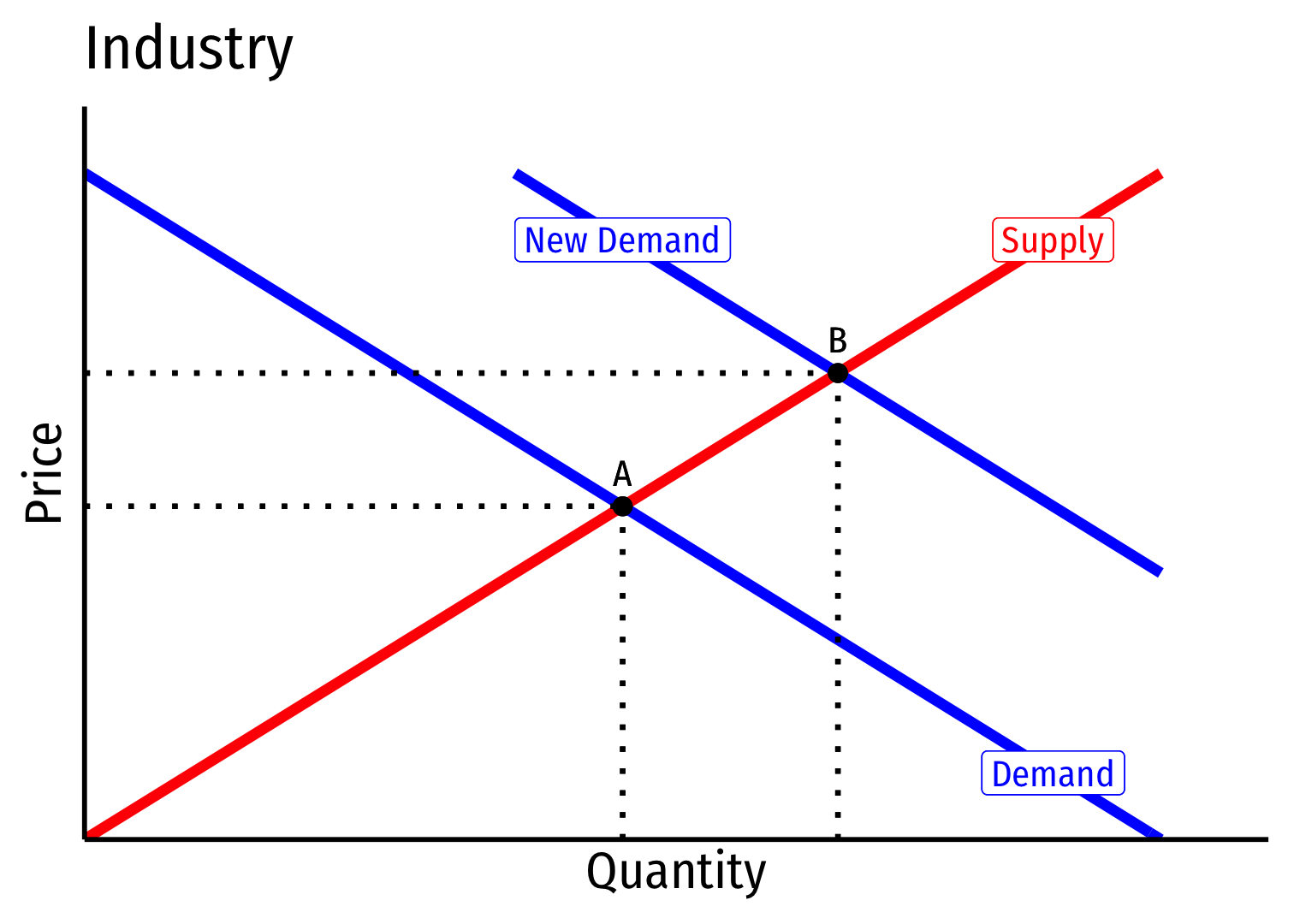
Long run: profit attracts entry \(\implies\) industry supply will increase
But more production lowers costs \((MC, AC)\) for all firms in industry
Decreasing Cost Industry (External Economies) VI
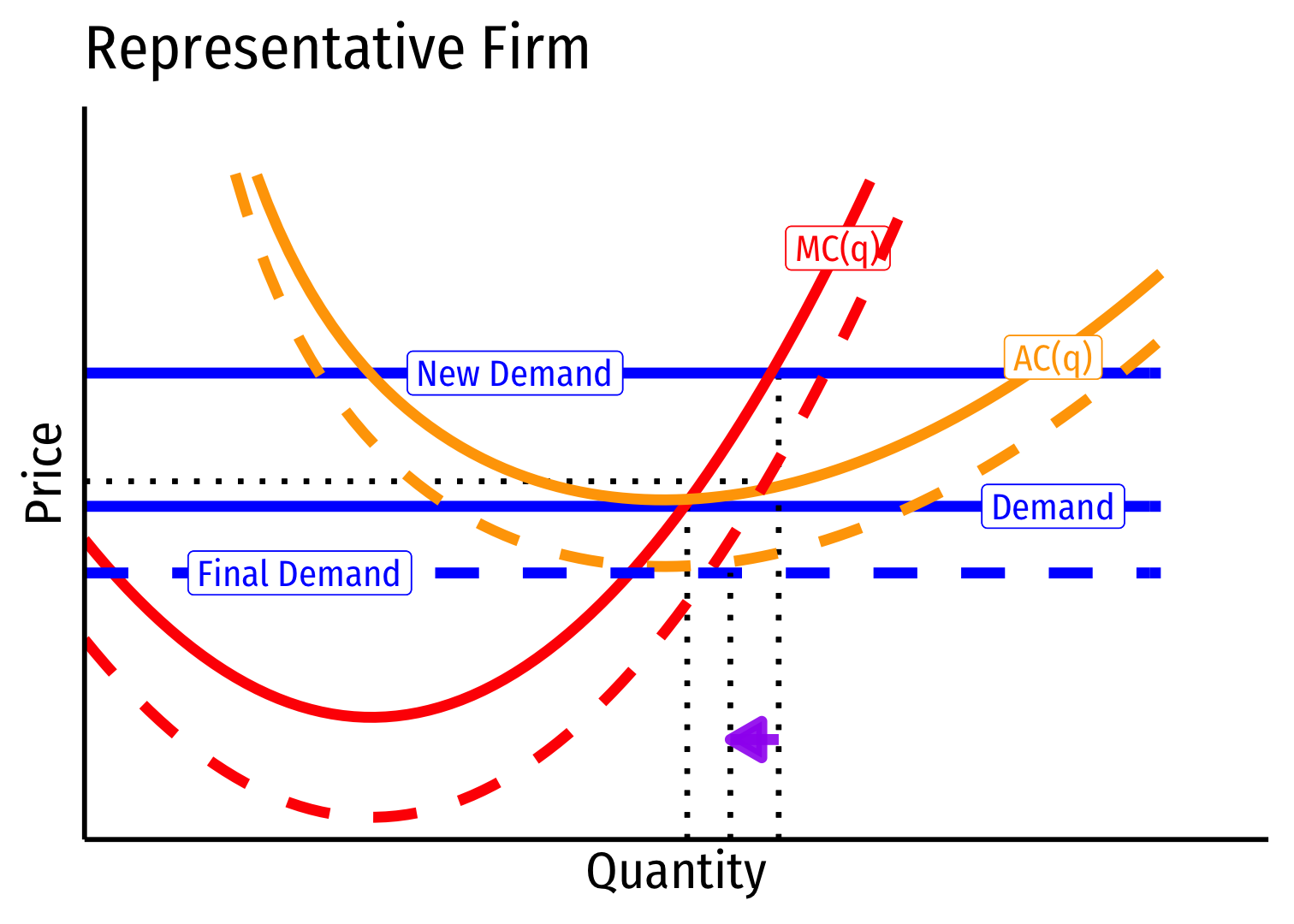
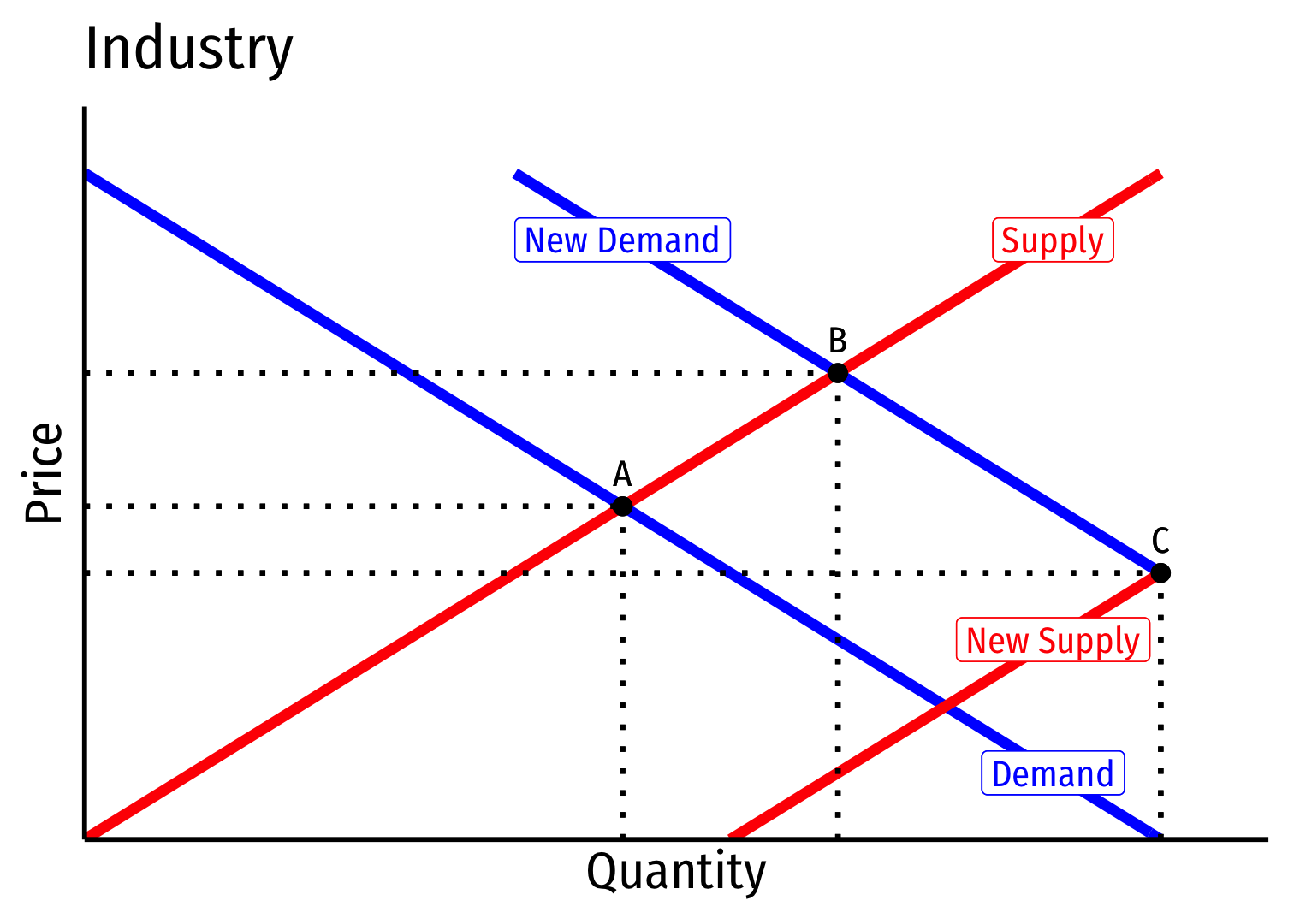
Long run \((B \rightarrow C)\): firms enter until \(\pi=0\) at \(p=AC(q)\)
Firms charge higher \(p^*\), producer lower \(q^*\), earn \(\pi=0\)
Decreasing Cost Industry (External Economies) VII
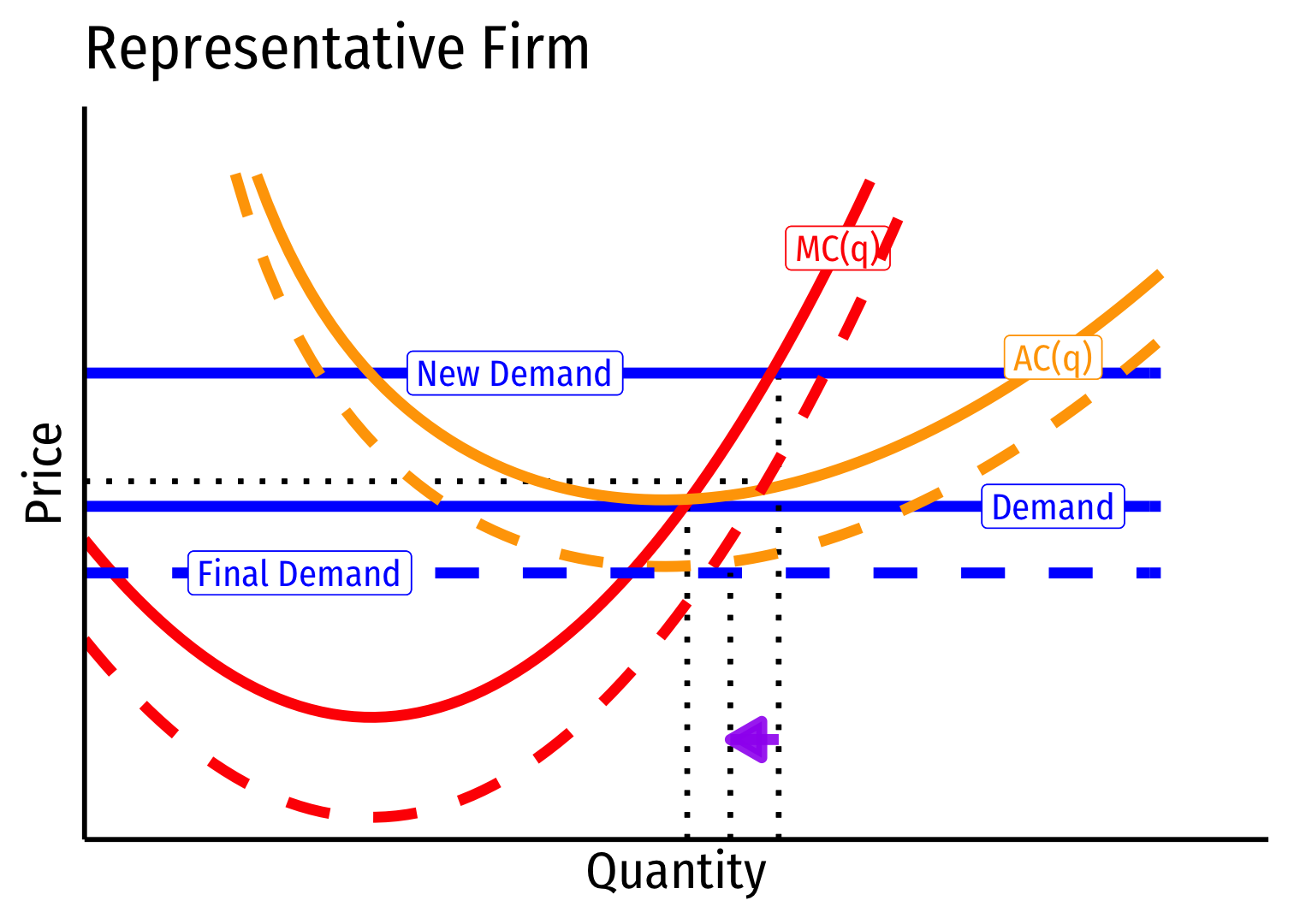
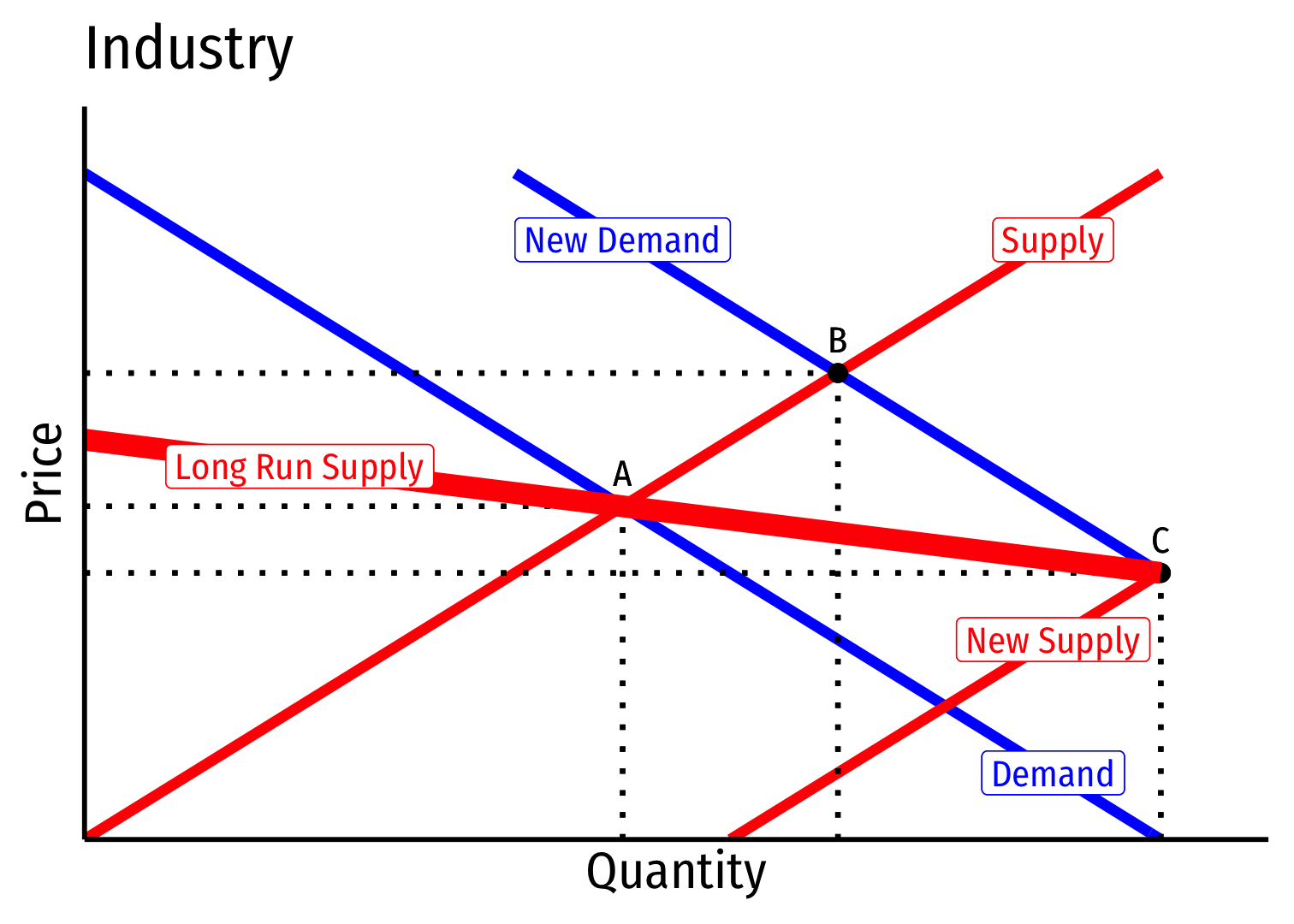
- Long run industry supply curve is downward sloping!
Comparing all Industry Types
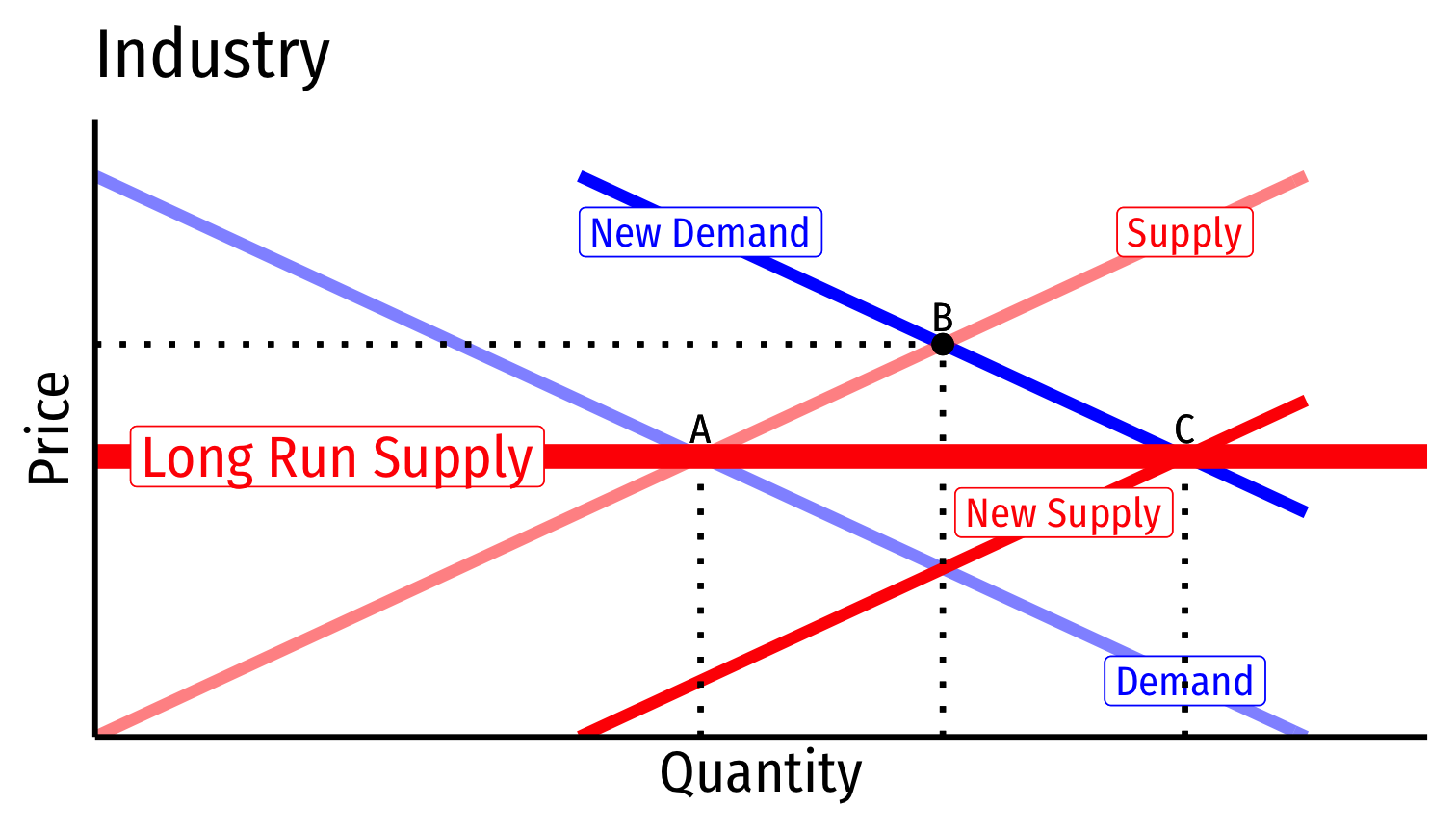
- Constant cost industry
- No external economies
- Increase in industry output has no effect on costs
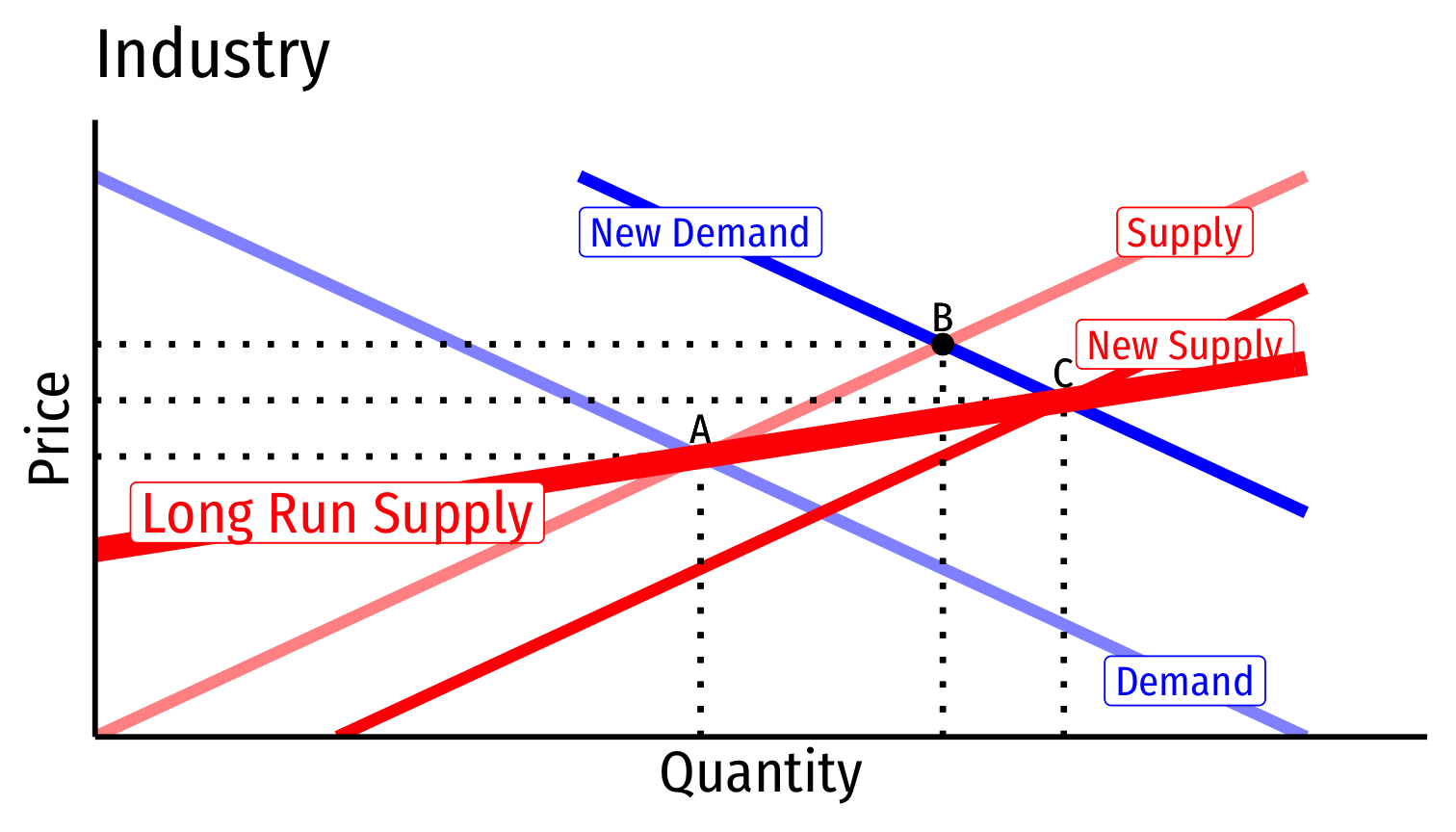
- Increasing cost industry
- External diseconomies
- Increase in industry output raises all firms’ costs
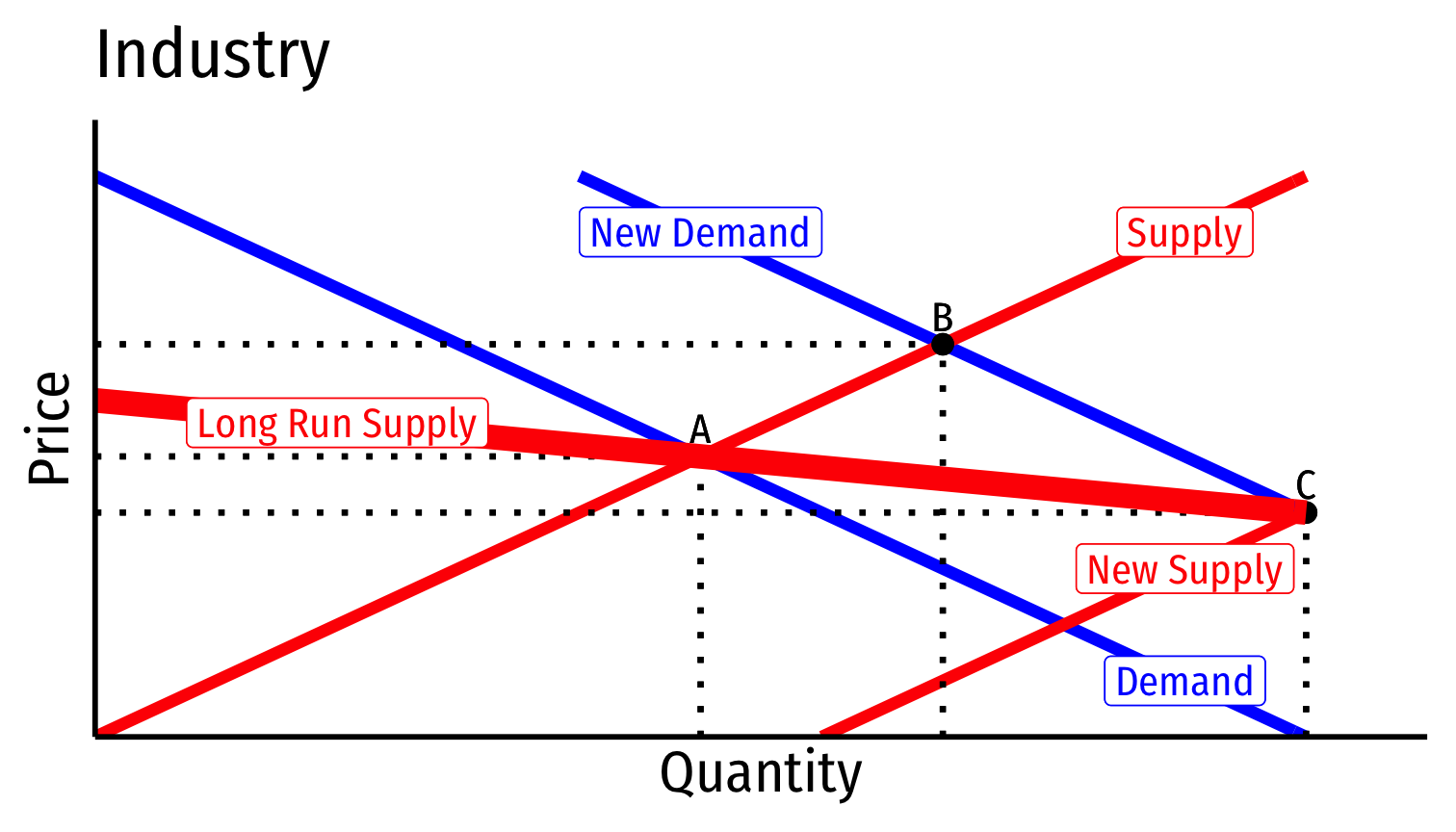
- Decreasing cost industry
- External economies
- Increase in industry output lowers all firms’ costs
Supply Functions
Supply Function
- Supply function relates quantity to price
Example: $$q=2p-4$$
- Not graphable (wrong axes)!
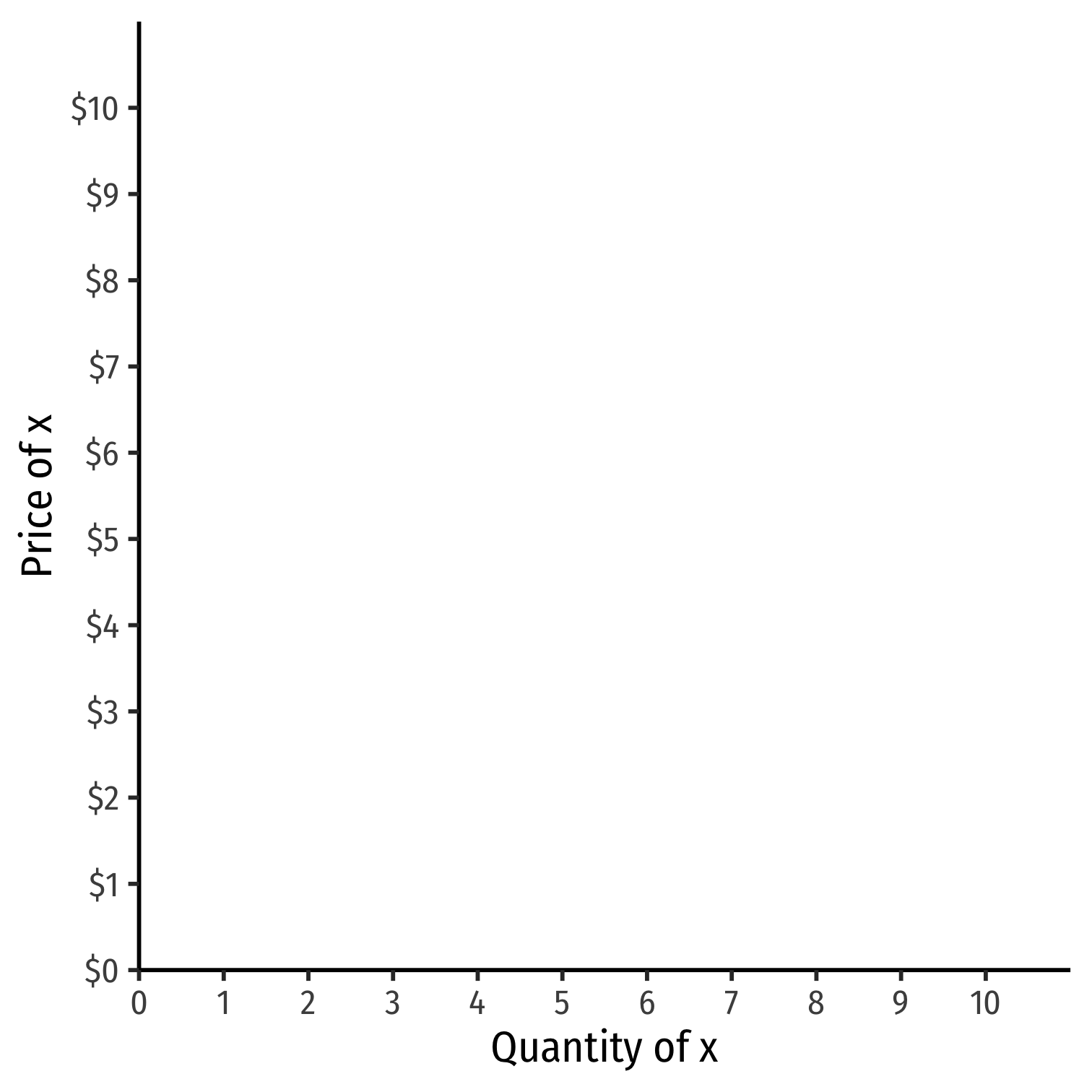
Inverse Supply Function
- Inverse supply function relates price to quantity
- Take supply function, solve for \(p\)
Example: $$p=2+0.5q$$
- Graphable (price on vertical axis)!
Inverse Supply Function
- Inverse supply function relates price to quantity
- Take supply function, solve for \(p\)
Example: $$p=2+0.5q$$
- Graphable (price on vertical axis)!

Inverse Supply Function
Example: $$p=2+0.5q$$
Slope: 0.5
Vertical intercept called the "Choke price": price where \(q_S=0\) ($2), just low enough to discourage any sales
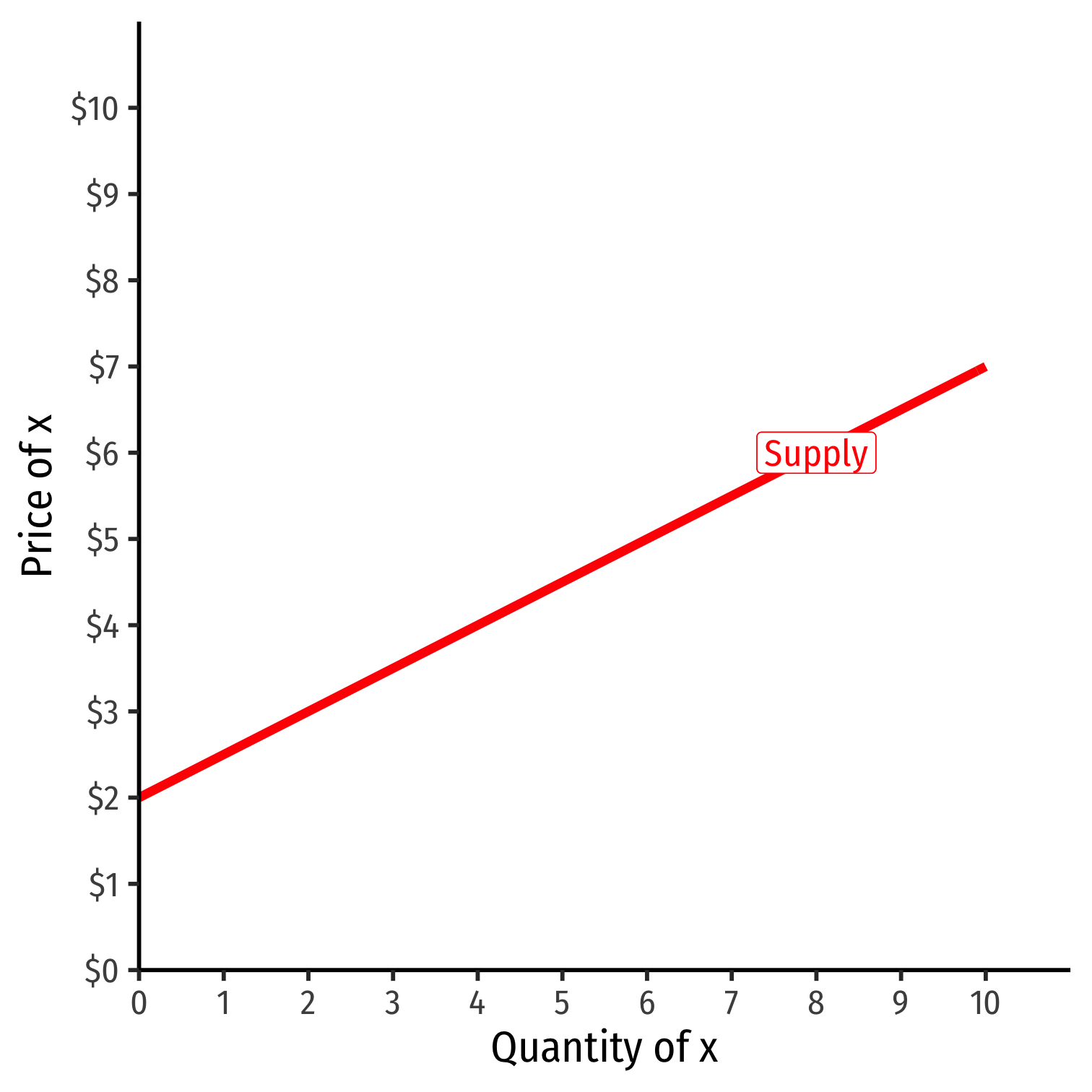
Inverse Supply Function
Read two ways:
Horizontally: at any given price, how many units firm wants to sell
Vertically: at any given quantity, the minimum willingness to accept (WTA) for that quantity

Price Elasiticity of Supply
Price Elasticity of Supply
- Price elasticity of supply measures how much (in %) quantity supplied changes in response to a (1%) change in price
$$\epsilon_{q_S,p} = \frac{\% \Delta q_S}{\% \Delta p}$$

Price Elasticity of Supply: Elastic vs. Inelastic
$$\epsilon_{q_S,p} = \frac{\% \Delta q_S}{\% \Delta p}$$
| “Elastic” | “Unit Elastic” | “Inelastic” | |
|---|---|---|---|
| Intuitively: | Large response | Proportionate response | Little response |
| Mathematically: | \(\vert \epsilon_{q_s,p}\vert > 1\) | \(\vert \epsilon_{q_s,p}\vert = 1\) | \(\vert \epsilon_{q_s,p} \vert < 1\) |
| Numerator \(>\) Denominator | Numerator \(=\) Denominator | Numerator \(<\) Denominator | |
| 1% change in \(p\) causes | More than 1% change in \(q_s\) | Exactly 1% change in \(q_s\) | Less than 1% change in \(q_s\) |
Compare to price elasticity of demand
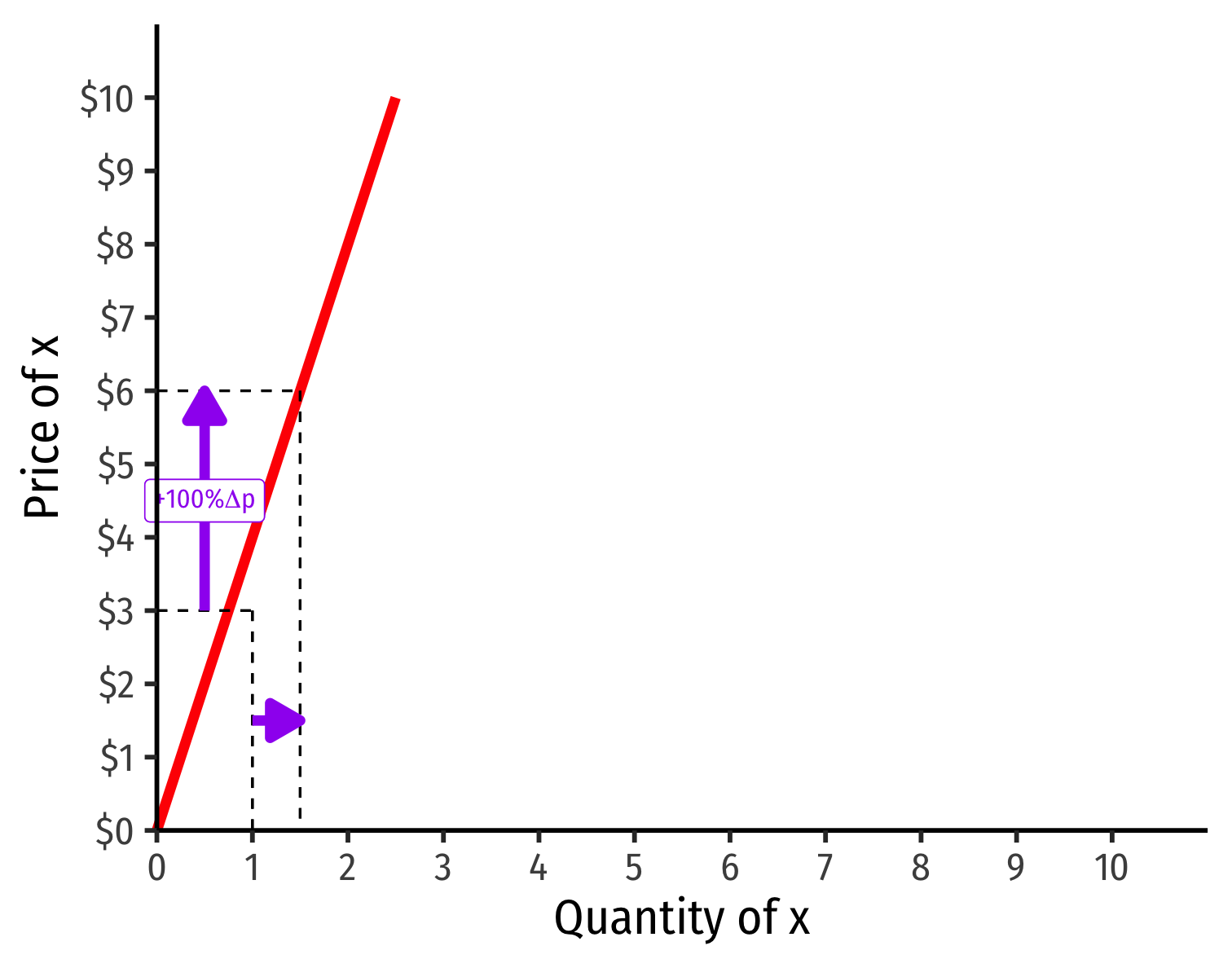
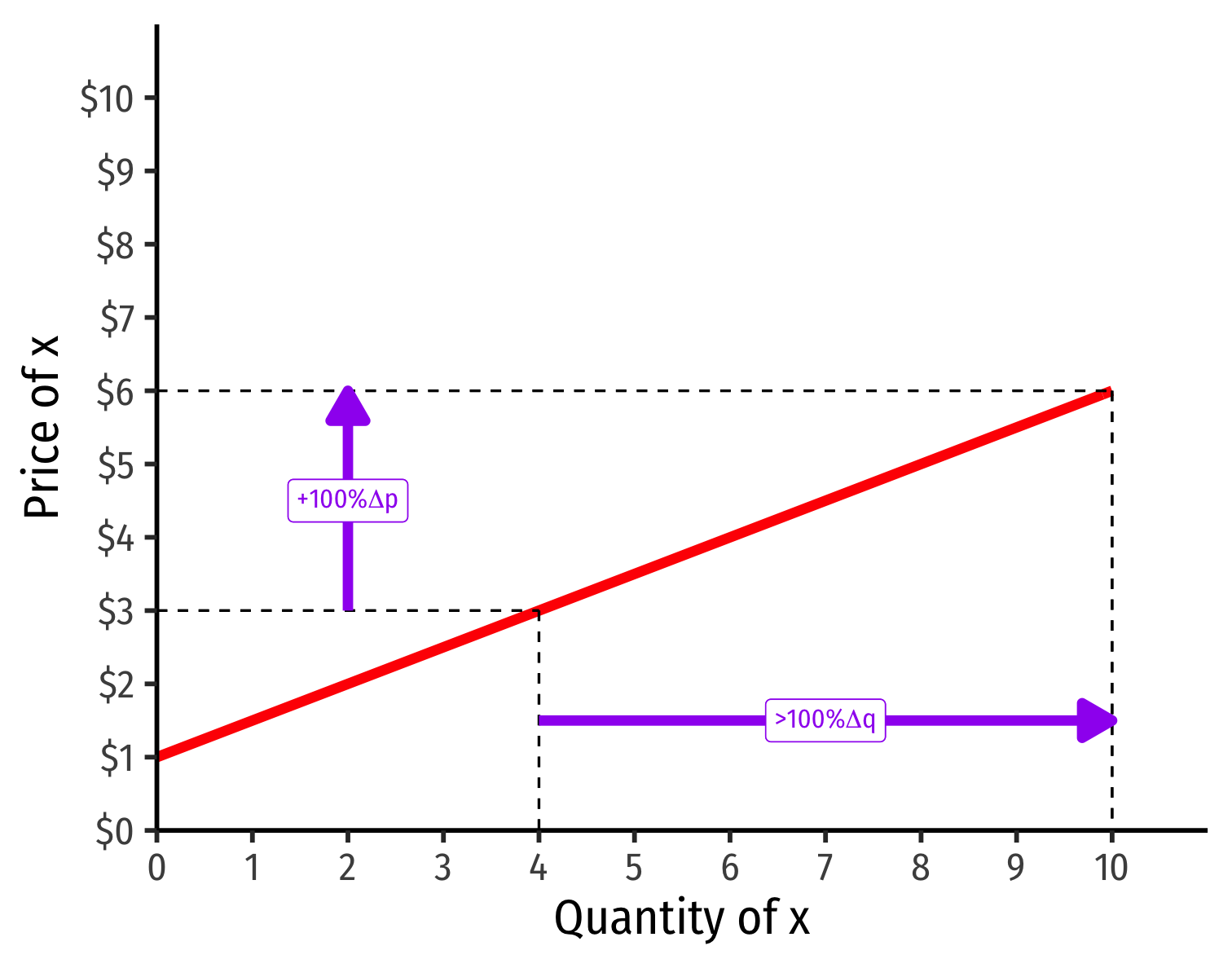
Visualizing Price Elasticity of Supply
An identical 100% price increase on an:
“Inelastic” Supply Curve
“Elastic” Supply Curve
Price Elasticity of Supply Formula
$$\color{red}{\epsilon_{q,p} = \mathbf{\frac{1}{slope} \times \frac{p}{q}}}$$
First term is the inverse of the slope of the inverse supply curve (that we graph)!
To find the elasticity at any point, we need 3 things:
- The price
- The associated quantity supplied
- The slope of the (inverse) supply curve

Example
Example: The supply of bicycle rentals in a small town is given by:
$$q_S=10p-200$$
Find the inverse supply function.
What is the price elasticity of supply at a price of $25.00?
What is the price elasticity of supply at a price of $50.00?
Price Elasticity of Supply Changes Along the Curve
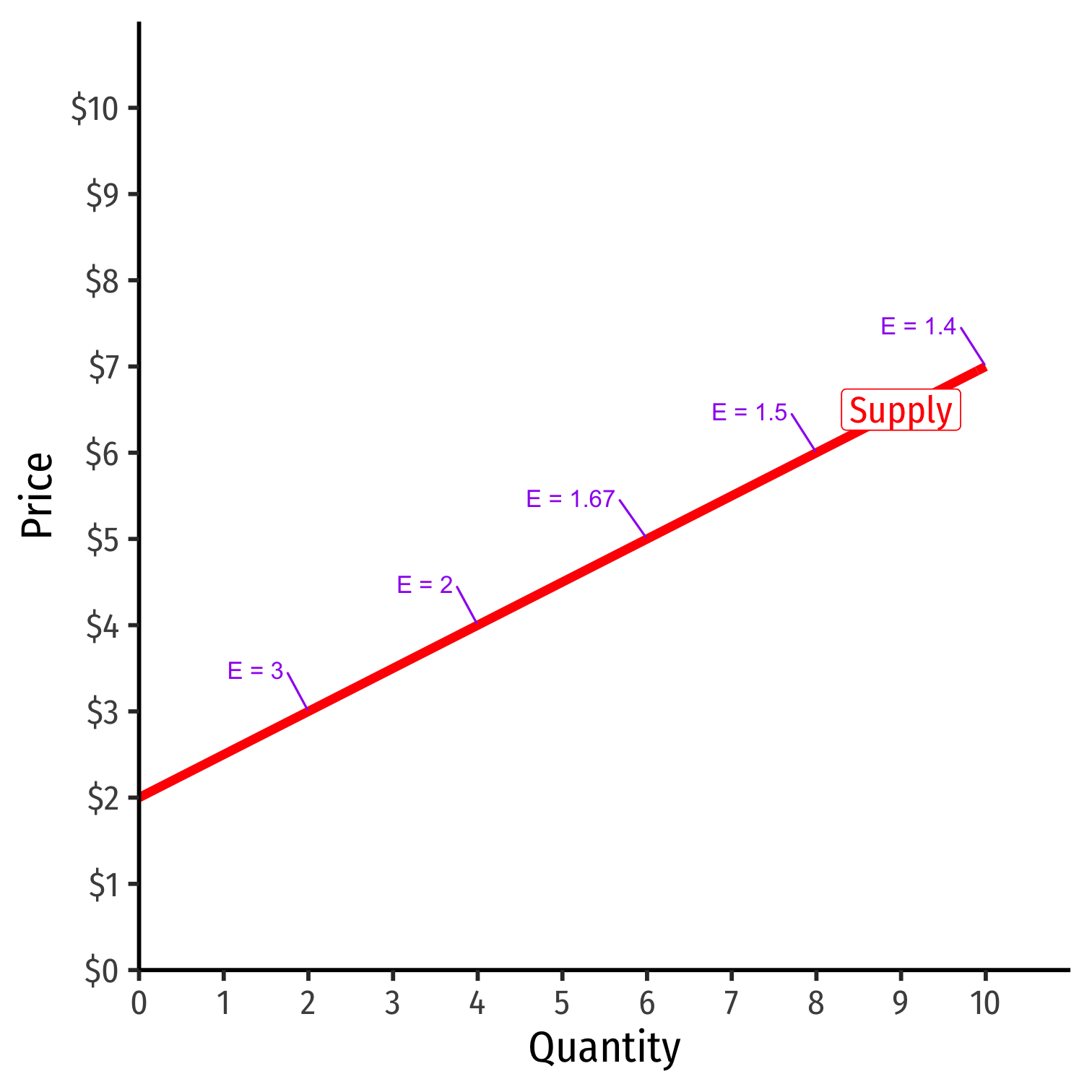
$$\epsilon_{q,p} = \mathbf{\frac{1}{slope} \times \frac{p}{q}}$$
Elasticity \(\neq\) slope (but they are related)!
Elasticity changes along the supply curve
Often gets less elastic as \(\uparrow\) price \((\uparrow\) quantity)
- Harder to supply more
Determinants of Price Elasticity of Supply I
What determines how responsive your selling behavior is to a price change?
The faster (slower) costs increase with output \(\implies\) less (more) elastic supply
- Mining for natural resources vs. automated manufacturing
Smaller (larger) share of market for inputs \(\implies\) more (less) elastic
- Will your suppliers raise the price much if you buy more?
- How much competition is there in your input markets?

Determinants of Price Elasticity of Supply II
What determines how responsive your selling behavior is to a price change?
- More (less) time to adjust to price changes \(\implies\) more (less) elastic
- Supply of oil today vs. oil in 10 years

Price Elasticity of Supply: Examples
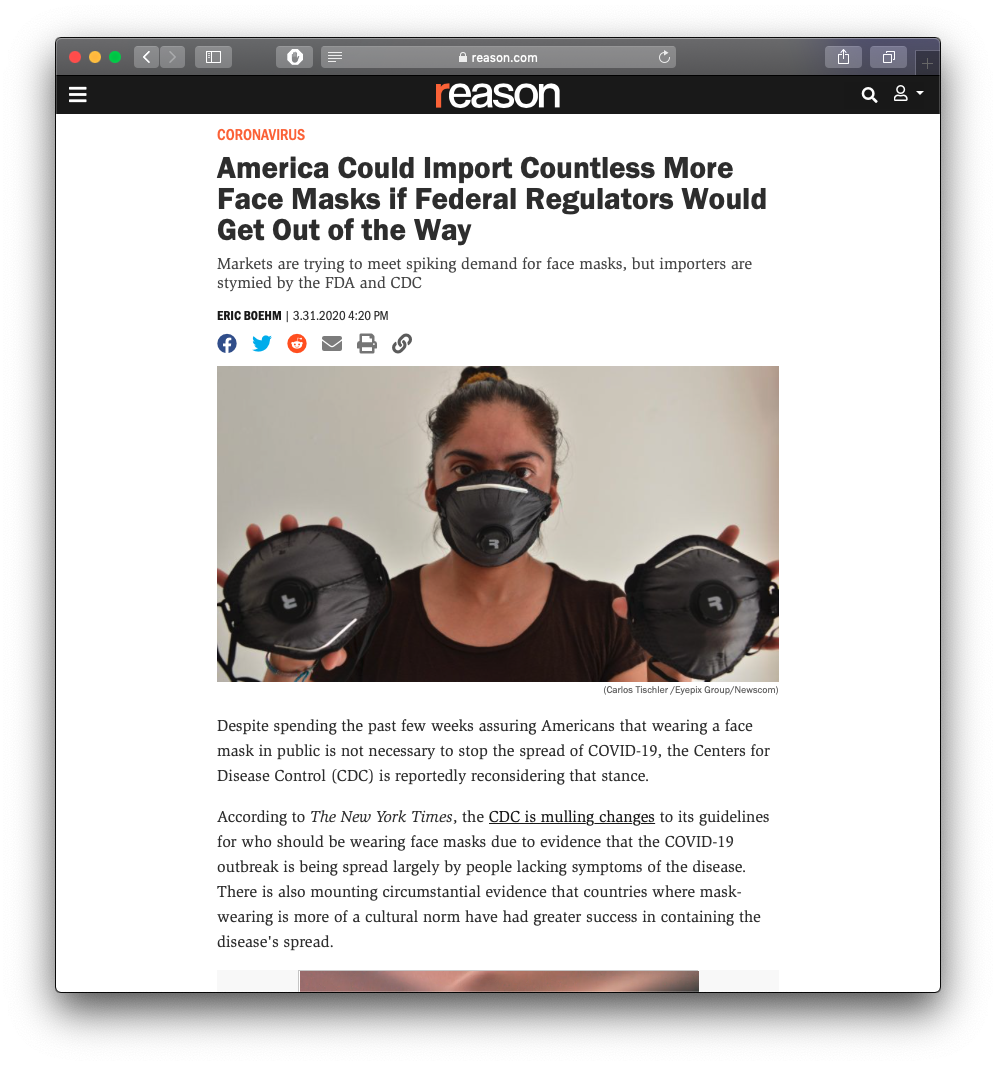
A report by @PIIE found an N-95 respirator mask still faces a 7% U.S. tariff.
— Chad P. Bown (@ChadBown) April 21, 2020
Remaining US duties include
• 5% on hand sanitizer
• 4.5% on protective medical clothing
• 2.5% on goggles
• 6.4-8.3% on other medical headwear
By @ABehsudi 1/https://t.co/LcxE0FFlXO
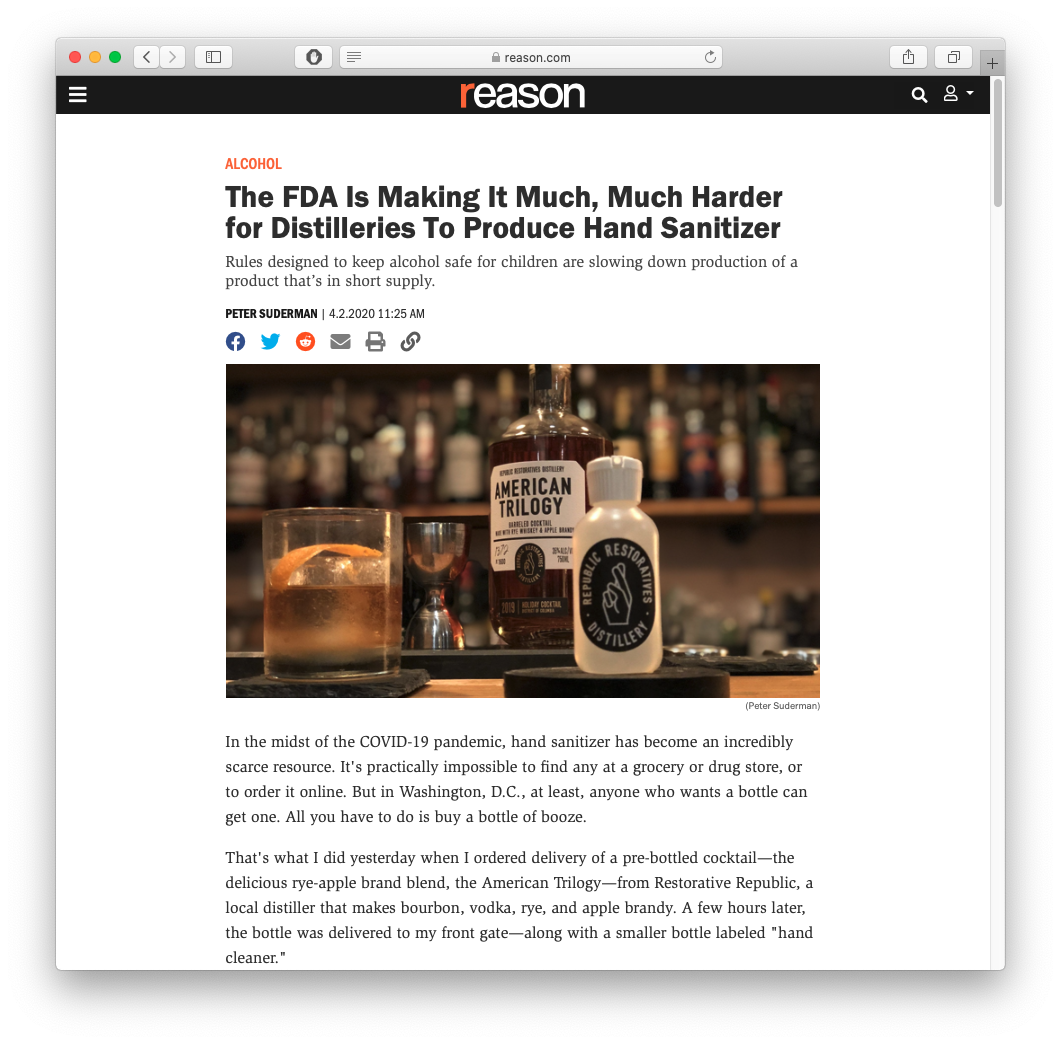
Price Elasticity of Supply: Examples

Source: Washington Post (Oct 2, 2021): “Inside America’s Broken Supply Chain”
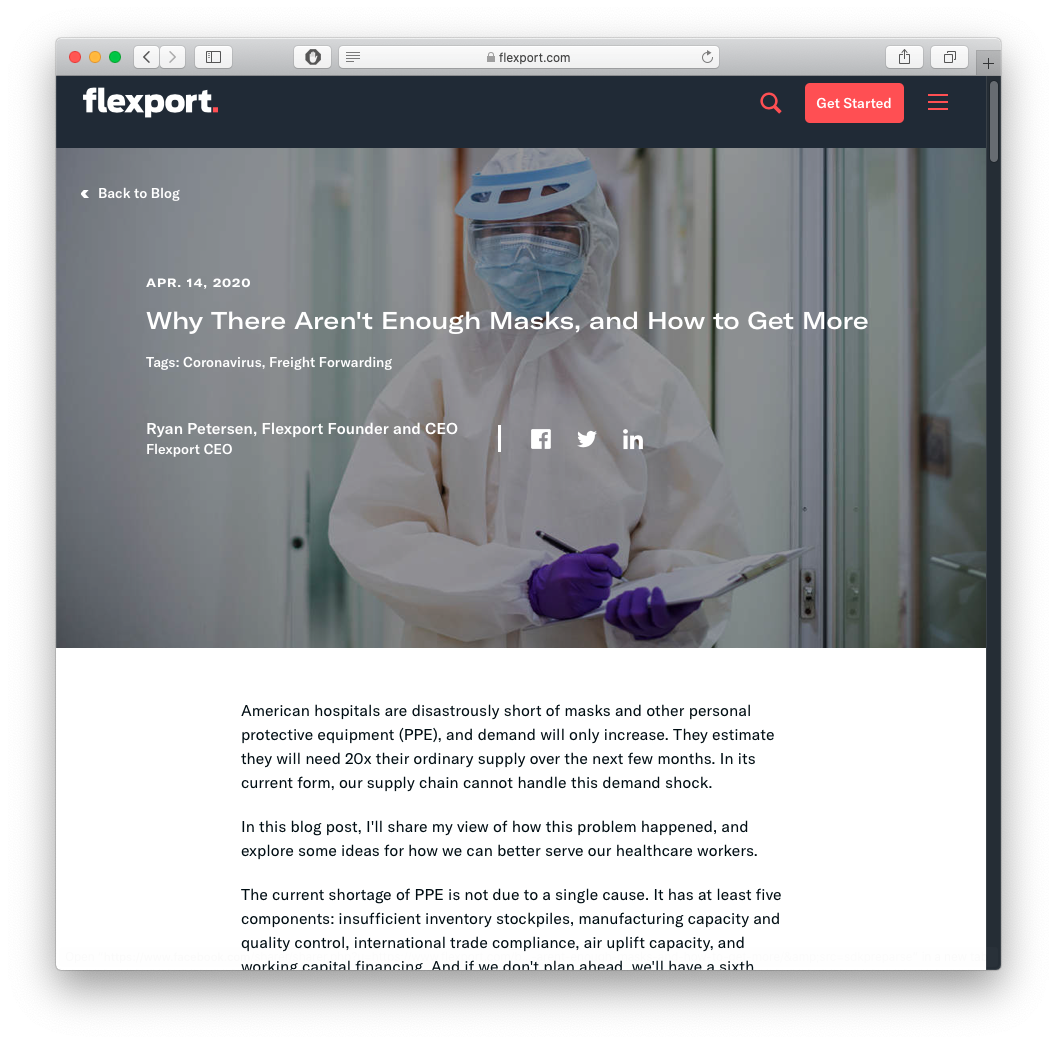
Price Elasticity of Supply: Examples
Yesterday I rented a boat and took the leader of one of Flexport's partners in Long Beach on a 3 hour of the port complex. Here's a thread about what I learned.
— Ryan Petersen (@typesfast) October 22, 2021