Problem Set 6

UNGRADED: For final exam practice only!

Answers

Concepts and Critical Thinking

Please answer the following questions briefly (1-3 sentences). Use examples as necessary. Be sure to label graphs fully, if appropriate.

Question 1

Compare and contrast the features of

1. perfect competition
1. monopoly
1. oligopoly
1. monopolistic competition

Rank each of the above 4 market structures (from smallest/lowest to largest/highest) in terms of:

1. the number of firms
1. long-run market price
1. equilibrium industry output
1. consumer surplus
1. long-run economic profits
1. deadweight loss

Question 2

Indicate based on the given information whether an industry is likely perfectly competitive, monopolistically competitive, an oligopoly, or a monopoly:

Fairfax, Virginia has three movie theaters
Restaurants in the greater Piedmont area, with many different cuisines to choose from
All of Connecticut gets its electricity from Connecticut Light & Power company
Laptops, where you can choose from many different brands (Acer, Asus, Gateway, Toshiba, Sony, HP, Dell, IBM, Lenovo, etc) and each is slightly different
Wheat in the U.S., provided by many small farmers, with each farmer’s wheat being identical to every other farmer’s wheat
The music industry, where Universal, Sony, EMI, and Warner account for 87% of the market

Question 3

Indicate which good is more likely to have a higher markup for firms with market power in these industries, and why:

Alcohol or jewelry
Prescription drugs or televisions
Gym memberships or school supplies
Doughnuts or bread
Popcorn in a movie theater or popcorn from a street vendor

Question 4

Describe the conditions required to make a market contestable. Describe and compare the Nash equilibrium of a contestable market with a pure monopoly, and with perfect competition.

Question 5

Explain what a cartel is, and comment on their stability.

Problems

Show all work for calculations. You may lose points, even if correct, for missing work. Be sure to label graphs fully, if appropriate.

Question 6

Consider the following Entry game in normal form. Suppose there are two firms, each of whom can choose to Enter a market, or Stay Out. If both firms enter, they split the market, each earning $50. I f b o t h s t a y o u t, e a c h f i r m e a r n s$ 0. If one enters and the other stays out, the entrant can act as a monopolist and earns $100, w i t h t h e o t h e r f i r m e a r n i n g$ 0.

What is the Nash Equilibrium of this game?

Question 7

Suppose you are a restaurant in a monopolistically competitive industry. Your firm has a constant marginal and average cost at $4 per unit.

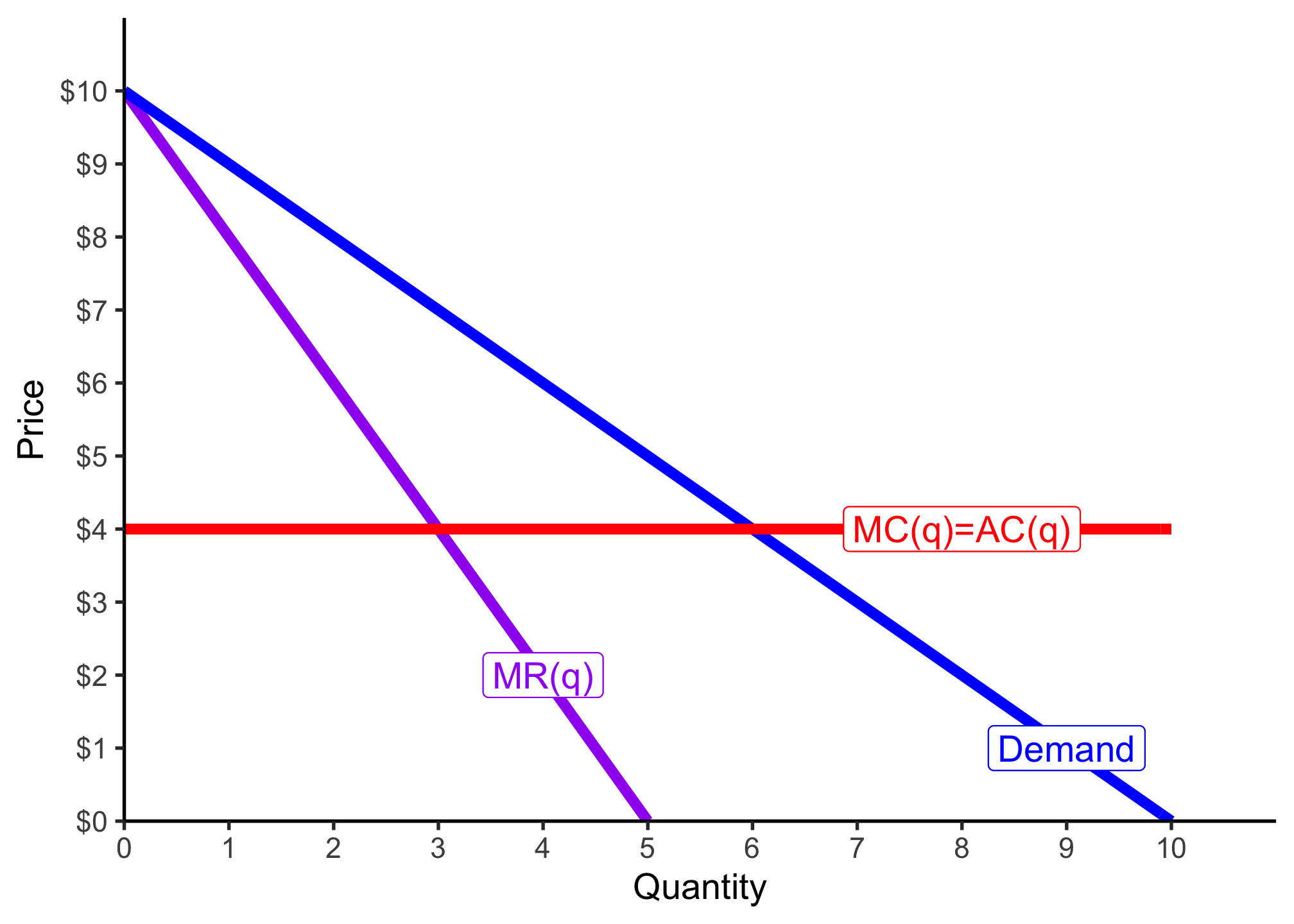
Part A

If this were a perfectly competitive market, what would be the market price and equilibrium quantity?

Part B

Calculate the (i) consumer surplus, (ii) profit, and (iii) deadweight loss at this price and quantity. Show these on the graph.

Part C

Now suppose this firm has market power from a barrier to entry, and can operate like a monopolist. What price and quantity does it set?

Part D

Calculate the (i) consumer surplus, (ii) profit, and (iii) deadweight loss at this price and quantity. Show these on the graph.

Part E

Now suppose that the firm had earned this market power via rent-seeking. From its lobbying efforts, it had convinced the local government to require all new restaurants to get a special license, making it harder for new entrants to compete in the market. What was the most that this firm was willing to spend on lobbying in order to get the license requirement?

Part F

If there are 10 identical (in terms of costs and size, if not food or brand) restaurants in the industry, and all engage in maximal rent-seeking to obtain the license, what is the true total cost of market power in this market to society?

Question 8

You are a producer of smartphones and have some market power. You have a cost structure:

$\begin{aligned} C (q) & = 10 q^{2} + 200 q + 1000 \\ M C (q) & = 20 q + 200 \end{aligned}$

You estimate the demand for your smartphones to be: $q = 100 - 0.2 p$ where $q$ is millions of smartphones.

Part A

Find the function for your marginal revenues.

Part B

How many smartphones should you produce, and at what price, to maximize your profit?

Part C

What is the cost per smartphone at the quantity you are producing?

Part D

What is your total profit?

Part E

What would be the lowest possible price you would need to charge to break even?

Part F

How much of your price is markup over marginal cost?

Part G

Calculate the elasticity of demand at your profit-maximizing price.

Question 9

Suppose that the market demand for bentonite is given by $q = 40 - 0.5 p$

where $q$ tons of bentonite per day and $p$ is the price per ton. Bentonite is produced by a monopolist at a constant marginal and average total cost of $10 per ton.

Part A

Find the marginal revenue curve for the monopolist.

Part B

Find the profit-maximizing level of output and price.

Part C

How much profit does the monopolist earn?

Part D

How much of the price is markup over marginal cost?

Part E

Calculate the elasticity of demand at the profit-maximizing price.

Question 10

Consider a boat rental firm on a popular beach that has a constant average and marginal cost of $30 per boat hire. It has estimated that demand from Locals $(L)$ and demand from Tourists $(T)$ are: $\begin{aligned} q_{L} & = 40 - 0.4 p \\ q_{T} & = 25 - 0.1 p \end{aligned}$

Part A

Suppose it must charge a single price to all customers. Find the profit-maximizing quantity, price, and the total profits.

Part B

How much of the price is markup?

Part C

What is the price elasticity of demand at this price?

Part D

Now suppose the firm is able to segment the market and charge different prices to Tourists and Locals. Find the profit-maximizing quantity, price, and the total profits.

Part E

For each segment of the market: how much of the price is markup, and what is the price elasticity of demand at the optimal price? How did the price for each segment change from the single price (Part A), and why?

Last updated on May 4, 2022